
Статью подготовили специалисты образовательного сервиса Zaochnik.
RLC-контур. Свободные колебания
Содержание:
-контур
Кроме как в механических системах, к примеру, в таких, маятник или же грузило на пружине, свободные колебания могут возникать также и в электрических цепях, самым простым примером чего может послужить последовательный -контур, изображенный на рис.
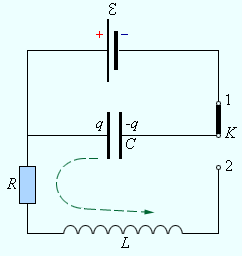
Рисунок Последовательный -контур.
Находясь в положении , ключ позволяет источнику зарядить конденсатор до некоего напряжения . Процесс разрядки ранее заряженного конденсатора провоцируется переключением ключа во второе положение и происходит через катушку индуктивности и резистор . При выполнении определенных условий данный процесс может приобретать характер колебательного.
Для не содержащей внешнего источника тока замкнутой -цепи закон Ома представляет из себя выражение:
.
В данной формуле – напряжение на конденсаторе, является обозначением заряда конденсатора, а – ток в цепи. Правой частью соотношения является выражение ЭДС самоиндукции катушки. В случае, когда заряд конденсатора берется как переменная величина, описывающее свободные колебания в -контуре уравнение может быть приведено к виду:
.
Для начала рассмотрим такую ситуацию, в которой электромагнитные потери энергии в контуре равны нулю. В таком случае:
.
Примем обозначение . Данным чуть выше уравнением описывается процесс незатухающих свободных колебаний в - контуре. Внешне оно полностью эквивалентно уравнению свободных колебаний груза на пружине в условиях отсутствующих сил трения. Аналогичный свободным механическим и электрическим колебаниям процесс изображен на рисунке На данной иллюстрации приводятся графики зависимости заряда смещения груза и конденсатора от положения равновесия, а также графики изменений тока и скорости груза за период колебаний.
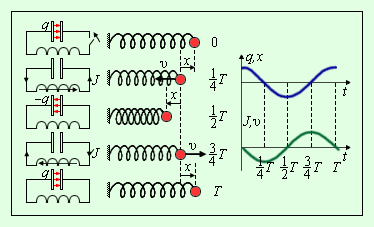
Рисунок Аналогия процессов свободных электрических и механических колебаний.
Сделать заключение о некой связи между механическими и электрическими величинами нам позволяет сопоставление процессов в электрическом колебательном контуре и свободных колебаний груза на пружине. Данные аналогии показаны в таблице.
| Электрические величины | Механические величины | ||
| Заряд конденсатора | Координата | ||
| Ток в цепи | Скорость | ||
| Индуктивность | Масса | ||
| Величина, обратная электроемкости | Жесткость | ||
| Напряжение на конденсаторе | Упругая сила | ||
| Энергия электрического поля конденсатора | Потенциальная энергия пружины | ||
| Магнитная энергия катушки | Кинетическая энергия | ||
| Магнитный поток | Импульс | ||
Свободные колебания
Свободные колебания в электрическом контуре носят название гармонических при условии отсутствия затухания.
Такие колебания происходят по закону:
.
Параметры и колебательного контура определяют лишь собственную частоту свободных колебаний:
«Начальными условиями», определяющими амплитуду и начальную фазу , называют тот способ, при помощи которого систему вывели из равновесия.
Например, для процесса колебаний, который начнется в контуре, изображенном на рисунке , после перевода ключа в второе положение, .
Процесс свободных колебаниях провоцирует повторяющееся превращение запасенной в конденсаторе электрической энергии в магнитную энергию катушки и наоборот. В ситуации, когда потери энергии равны нулю, полная электромагнитная энергия системы не претерпевает изменений:
Однако любой реально существующий контур, в отличие от идеального, включает в себя некоторое сопротивление . По этой причине, процесс свободных колебаний в подобном контуре не подчиняется гармоническому закону. Запасенная в контуре энергия с каждым периодом колебаний теряется, превращаясь в джоулево тепло, из-за чего колебания становятся затухающими (рис. ).
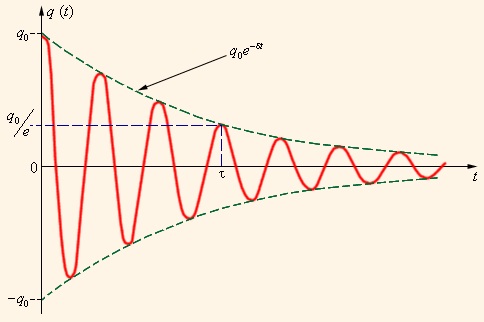
Рисунок Затухающие колебания в контуре.
Затухающие колебания в электрическом контуре сравнимы с затухающими колебаниями груза на пружине в условиях существующего вязкого трения, при котором сила трения меняет свое значение прямо пропорционально скорости тела: .
В данной формуле сопротивление электрического контура аналогично коэффициенту . Уравнение свободных колебаний в контуре при наличии затухания принимает следующий вид:
Коэффициентом затухания называется физическая величина .
Следующая функция представляет собой решение приведенного выше дифференциального уравнения:
,
Также она содержит описывающий затухание колебаний множитель . Скорость затухания зависит от электрического сопротивления контура.
Интервал времени , в течение которого амплитуда колебаний уменьшается в раза, называется временем затухания.
Понятие добротности колебательной системы:
,
где является числом полных колебаний, которые совершает система за время затухания .
Любая добротность , относящаяся к колебательной системе, которая способна совершать свободные колебания, имеет следующее энергетическое определение:
Добротность , принадлежащая -контуру, выражают формулой:
Добротность электрических контуров, которые применяются в радиотехнике, обычно порядка нескольких десятков и даже сотен.
Стоит обратить внимание на то, что собственная частота ω свободных колебаний в контуре с не самой высокой добротностью несколько уступает собственной частоте идеального контура с такими же значениями и . Однако при данным различием можно пренебречь.
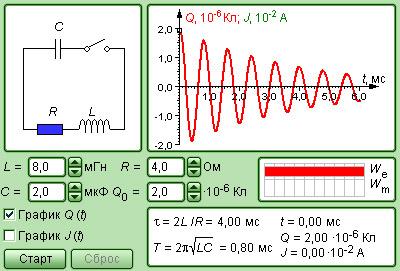
Рисунок Модель свободных колебаний в -контуре.
Навигация по статьям
