
Статью подготовили специалисты образовательного сервиса Zaochnik.
Затухающие колебания в контуре и их уравнение
Содержание:
Существуют колебания в системе без источника энергии, называемые затухающими. Рассмотрим реальный контур с сопротивлением не равным нулю. Для примера используют контур с включенным сопротивлением , с емкостью конденсатора , с катушкой индуктивности , изображенный на рисунке . Колебания, происходящие в нем, - затухающие.
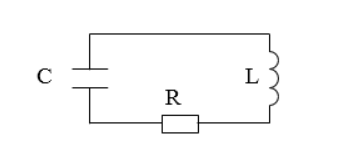
Рисунок
Именно наличие сопротивления становится главной причиной их затухания. Данный процесс возможен посредствам потерь энергии на выделение джоулева тепла. Аналог сопротивления в механике – действие сил трения.
Характеристики затухающих колебаний
Затухающие колебания характеризуют коэффициентом затухания . Применив второй закон Ньютона, получим:
Из записи видно, что действительно является характеристикой контура. Реже вместо применяют декремент затухания ,
Значение является амплитудой заряда, силы тока и так далее, равняется количеству колебаний, а - период времени уменьшения амплитуды в раз.
Для контура применима формула с частотой.
При небольшой говорят, что - собственная частота, отсюда .
При рассмотрении затухающих колебаний последовательного контура колебательный контур характеризуется добротностью :
, где и - сопротивление, индуктивность, емкость, а - частота резонанса. Выражение называют характеристическим или волновым сопротивлением. Для параллельного контура формула примет вид:
.
является входным сопротивлением параллельного контура.
Эквивалентное определение добротности применяется при слабых затуханиях. Его выражают через отношение энергий:
, называемое общей формулой.
Уравнения затухающих колебаний
Рассмотрим рисунок . Изменение заряда на конденсаторе в таком контуре описывается дифференциальным уравнением:
.
Если , то заряд конденсатора становится равным , и ток в цепи отсутствует.
Если изменения заряда не относят к колебаниям, разряд называют апериодическим.
Значение сопротивления, при котором колебания превращаются в апериодический разряд конденсатора, критическое .
.
Функция изображается аналогично рисунку .
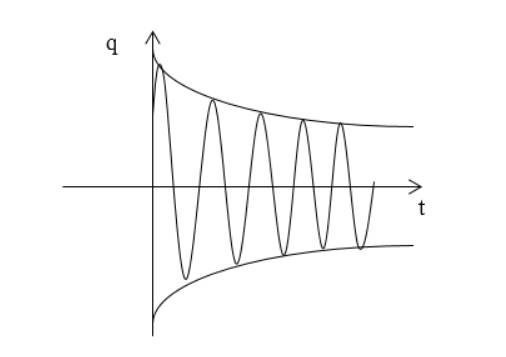
Рисунок
Записать закон убывания энергии, запасенной в контуре при с затухающими колебаниями. Обозначить коэффициент затухания в контуре , а собственную частоту - .
Решение
Отправная точка решения – это применение формулы изменения заряда на конденсаторе в - контуре:
.
Предположим, что при . Тогда применим выражение
.
Для нахождения :
, где .
Очевидно, что электрическая энергия запишется как:
.
Тогда значение магнитной энергии контура равняется:
.
Запись полной энергии будет иметь вид:
Где .
Ответ: .
Применив результат предыдущего примера, записать выражение для энергии, запасенной в контуре , при медленно затухающих колебаниях. Начертить график убывания энергии.
Решение
Если колебания в контуре затухают медленно, то:
.
Очевидно, выражение энергии, запасенной в контуре, вычислим из
, предварительно преобразовав до .
Такое упрощение возможно по причине выполнения условия , , что означает .
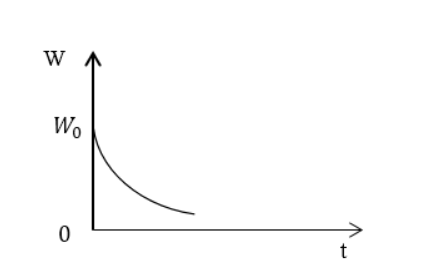
Рисунок
Ответ: . Энергия в контуре убывает по экспоненте.
Навигация по статьям
