
Статью подготовили специалисты образовательного сервиса Zaochnik.
Вынужденные колебания. Переменный ток
Содержание:
Дадим определение понятию вынужденных колебаний.
Вынужденные колебания – это процессы, которые происходят в электрических цепях под воздействием периодического источника тока.
Основным отличием вынужденных колебаний по сравнению с собственными колебаниями в электрических цепях является то, что они являются незатухающими. Неизбежные потери энергии компенсируются за счет внешнего источника периодического воздействия, который не позволяет колебаниям затухать.
Что такое переменный ток?
Переменный ток — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.
Рассмотрим случай, когда электрическая цепь способна совершать собственные свободные колебания с некоторой частотой . Предположим, что к этой цепи подключен внешний источник, напряжение которого изменяется по гармоническому закону с частотой .
Частота свободных колебаний в электрической сети будет определяться параметрами этой сети. Вынужденные колебания, которые установятся при подключении внешнего источника , будут происходить на частоте этого внешнего источника.
Частота вынужденных колебаний устанавливается не сразу после включения внешнего источника, а спустя некоторое время . По порядку величины это время будет равно времени затухания свободных колебаний в сети .
Цепи переменного тока
Цепи переменного тока – это такие электрические цепи, в которых под воздействием периодического источника тока происходят установившиеся вынужденные колебания.
Рассмотрим устройство колебательного контура, в который включен источник тока с напряжением, изменяющимся по периодическому закону:
где – амплитуда, – круговая частота.
Фактически, это будет -цепь.
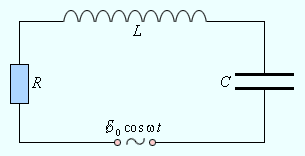
Рисунок Вынужденные колебания в контуре.
Будем считать, что для изображенной на этом рисунке электрической цепи выполняется условие квазистационарности. Это позволит нам записать закон Ома для мгновенных значений токов и напряжений:
Величину принято называть напряжением на катушке индуктивности. Фактически, это ЭДС самоиндукции катушки, которую мы для простоты вычислений перенесли с противоположным знаком в левую часть уравнения из правой.
Уравнение вынужденных колебаний можно записать в виде:
где и – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами и . Напряжения при установившихся вынужденных колебаниях изменяются с частотой внешнего источника переменного тока .
Векторная диаграмма токов и напряжений
Для решения уравнения вынужденных колебаний мы можем использовать достаточно наглядный метод векторных диаграмм. Для этого используем векторную диаграмму, на которой с помощью векторов изобразим колебания определенной заданной частоты .
Давайте посмотрим, как построить векторную диаграмму токов и напряжений.
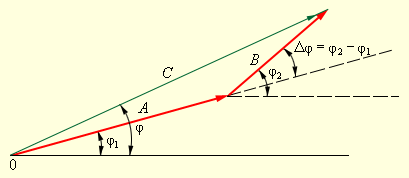
Рисунок Векторная диаграмма, на которой с помощью векторов изображены гармонические колебания и их суммы .
Наклон векторов к горизонтальной оси определяется фазой колебаний и , а длины векторов соответствуют амплитудам колебаний и . Относительный фазовый сдвиг определяет взаимную ориентацию векторов: . Для того, чтобы построить вектор, изображающий суммарное колебание, нам необходимо использовать правило сложения векторов: .
При вынужденных колебаниях в электрической цепи для построения векторной диаграммы напряжений и токов нам необходимо знать соотношения между амплитудами токов и напряжений и фазовый сдвиг между ними для любого участка цепи.
Источник переменного тока может быть подключен к:
- катушке индуктивности ;
- резистору с сопротивлением ;
- конденсатору с емкостью .
Рассмотрим эти три примера подробнее. Будем считать, что напряжение на резисторе, катушке и конденсаторе во всех трех случаях равно напряжению внешнего источника переменного тока.
Резистор в цепи переменного тока
Мы обозначили амплитуду тока, который протекает через резистор, через . Соотношение выражает связь между амплитудами тока и напряжения на резисторе. Фазовый сдвиг в этом случае равен нулю. Физическая величина – это активное сопротивление на резисторе.
Конденсатор в цепи переменного тока
Запишем формулу:
.
Соотношение между амплитудами тока и напряжения : .
Ток опережает по фазе напряжение на угол .
Физическая величина - это емкостное сопротивление конденсатора.
Катушка в цепи переменного тока
Запишем формулы:
Соотношение между амплитудами тока и напряжения : .
Ток отстает по фазе от напряжения на угол .
Физическая величина - это индуктивное сопротивление катушки.
Построим векторную диаграмму для последовательного -контура, частота вынужденных колебаний в котором ω.
При построении диаграммы будем учитывать, что через различные участки цепи протекает один и тот же ток. Удобнее делать это будет относительно вектора, который изображает колебания тока в цепи.
Для амплитуды тока введем обозначение . Фазу тока примем равной нулю, так как в данном случае нас интересуют не столько абсолютные значения фаз, сколько относительные фазовые сдвиги.
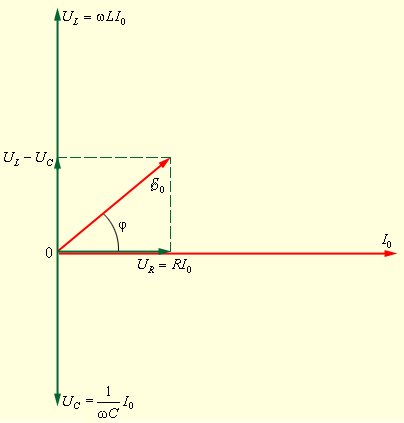
Рисунок Векторная диаграмма для последовательной -цепи.
Данная диаграмма построена для случая, когда или .
По фазе напряжение внешнего источника опережает ток, который течет в цепи, на некоторый угол .
Из рисунка видно, что
, откуда следует, что
.
Из выражения для видно, что амплитуда тока принимает максимальное значение при условии
или .
Понятие электрического резонанса
Электрический резонанс – это физическое явление возрастания амплитуды колебаний тока в случае совпадения частоты колебаний внешнего источника и собственной частоты электрической цепи .
При резонансе .
При резонансе сдвиг фаз φ между приложенным напряжением и током в цепи равен нулю. Если речь идет о последовательной -цепи, то такой резонанс называется резонансом напряжения.
С помощью векторной диаграммы явление резонанса можно исследовать аналогичным образом при другой последовательности элементов. Параллельное соединение элементов и позволяет получить резонанс токов.
При последовательном резонансе амплитуды и напряжений на конденсаторе и катушке резко возрастают: .
Ранее было введено понятие добротности -контура: .
Таким образом, при резонансе амплитуды напряжений на конденсаторе и катушке в раз превышают амплитуду напряжения внешнего источника.
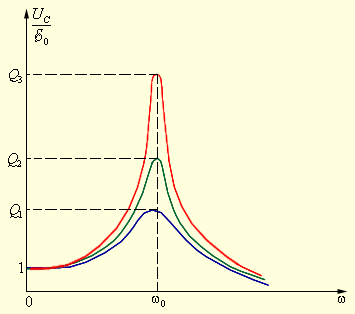
Рисунок Резонансные кривые для контуров с различными значениями добротности .
Рисунок иллюстрирует процессы, происходящие в последовательном электрическом контуре, а также зависимость между такими величинами как амплитуды напряжения на конденсаторе к амплитуде напряжения источника от его частоты ω для различных значений добротности . В контурах с низкой добротностью максимум резонансных кривых сдвинут в область низких частот.
Навигация по статьям
