Закон Ома для цепи переменного тока. Мощность

$R{I}_R=U_R; \frac{1}{\omega C}{I}_C=U_C; \omega L{I}_L=U_L$.

Указанные выше формулы внешне могут напоминать закон Ома  на участке цепи постоянного тока, но стоит заметить, что в этом случае вместо величин постоянных токов и напряжений на участке цепи, в них входят амплитудные значения напряжений и переменных токов.

Формулы, указанные выше, выражают собой закон Ома для переменного тока, который содержит один из элементов $R$, $L$ и $C$.

Движение переменного тока по участку цепи провоцирует электромагнитное поле выполнять работу, благодаря чему выделяется джоулево тепло.

Прикладной интерес у нас вызывает среднее значение мощности за некоторый период переменного тока:

$P=P_{c\alpha }=I_0{U}_0\overline{\cos \omega t \cos \left(\omega t+\phi \right)}$.

В приведенной выше формуле $I_0$ и $U_0$ являются амплитудными значениями тока и напряжения на выбранном участке цепи, а $\phi$ – фазовым сдвигом между током и напряжением. Черта же представляет собой символ усреднения. В случае, когда цепь содержит только резистор с сопротивлением $R$, то фазовый сдвиг $\phi$ будет равен нулю: 

$P_R=I_R{U}_R\overline{{\cos }^2\omega t}=\frac{I_R{U}_R}{2}=\frac{I_R^{2}R}{2}$.

Действующие значения силы тока и напряжения

Мощность переменного тока на участке цепи

Если в цепи содержится лишь конденсатор емкости $C$, то $\phi =\frac{\pi }{2}$. Отсюда, справедливо следующее выражение:

$P_C=I_C{U}_C\overline{\cos \omega t \cos \left(\omega t+\frac{\pi }{2}\right)}=I_C{U}_C\overline{\cos \omega t\left(-\sin \omega t\right)}=0.$

Таким же способом можно проиллюстрировать, что $PL=0$.

Исходя из описанного выше получим следующие определение.

Теперь стоит рассмотреть электрическую цепь, включающую последовательно соединенные резистор, конденсатор и катушки, и подключенную к источнику переменного тока некой частоты $\omega$. Следует выделить, что на всех участках цепи, соединенных последовательно, проходит один и тот же ток. Между напряжением внешнего источника $e\left(t\right)$ и током $J\left(t\right)$ проявляется фазовый сдвиг на определенный угол $\phi$.

Исходя из приведенных выше фактов, мы можем записать:

$J\left(t\right)=I_0\cos \omega t; e\left(t\right)={\delta }_0\cos \left(\omega t+\phi \right)$.

Данные формулы мгновенных значений тока и напряжения подходят к построениям, выполненным на векторной диаграмме (рис. $2.3.2$).

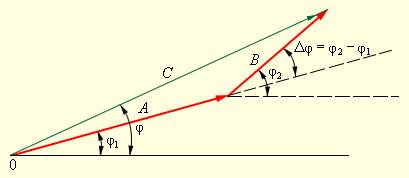
Рисунок $2.3.2.$ Гармонические колебания $A \cos (\omega t+{\phi }_1), B \cos (\omega t+{\phi }_2)$ и их суммы $C \cos (\omega t+\phi )$ на векторной диаграмме.

Средняя величина мощности, развиваемой источником переменного тока, может быть найдена из следующего выражения:

$P=I_0{\delta }_0\overline{\cos \omega t \cos \left(\omega t+\phi \right)}=\frac{I_0{\delta }_0}{2}\cos \phi =I_{Д}{\delta }_{Д} \cos \phi$.

Исходя из данных векторной диаграммы можно заявить, что $U_R={\delta }_0·\cos \phi$, следовательно,
$P=\frac{I_0{U}_R}{2}$, а вся мощность, которую развивает источник питания, теряется в виде джоулева тепла на резисторе.

В прошлых темах нами было получено выражение, являющееся соотношением амплитуд тока $I_0$ и напряжений ${\delta }_0$ в условиях последовательной $RLC$-цепи: 

$I_0=\frac{{\delta }_0}{\sqrt{R^2+{\left(\omega L-{\displaystyle \frac{1}{\omega C}}\right)}^2}}$

Закон Ома в условиях параллельной $RLC$-цепи

В различных расчетах, связанных с работой над цепями переменного тока, очень важное место занимает понятие полного сопротивления. Для его определения в цепи в большей части случаев практично использовать метод векторных диаграмм. В качестве примера, приведем параллельный подключенный к внешнему источнику переменного тока (рис. $2.4.1$) $RLC$-контур:

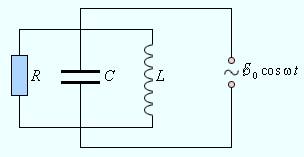
Рисунок $2.4.1.$ Параллельный $RLC$-контур.

При построении диаграммы важно учесть, что в условиях параллельного соединения напряжение на всех элементах $R$, $C$ и $L$ идентично и равняется напряжению внешнего источника питания. Ток, текущий в разных ветвях цепи, различается не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Следовательно, полное сопротивление цепи невозможно вычислить опираясь на законы параллельного соединения цепей постоянного тока. Векторную диаграмму для параллельного $RLC$-контура можно увидеть на рис. $2.4.2.$

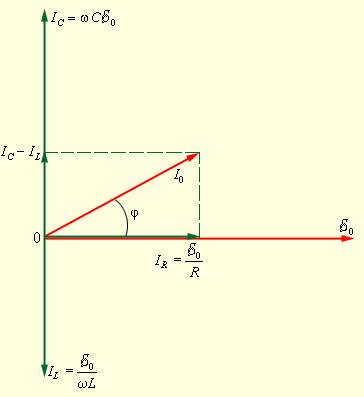
Рисунок $2.4.2.$ Векторная диаграмма для параллельного $RLC$-контур.

Исходя из вида диаграммы, следует:

$I_0={\delta }_0\sqrt{{\left(\frac{1}{R}\right)}^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}$.