Тонкие линзы

Линза - это составляющая часть почти каждого оптического прибора. Линзы бывают по своему определению собирающие и рассеивающие (рис. $3.3.1$).

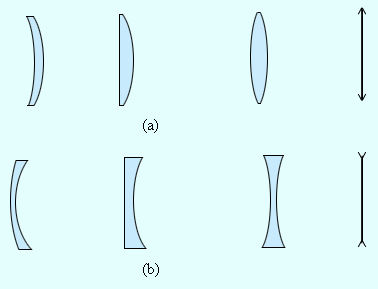
Рисунок $3.3.1.$ Собирающие $\left(a\right)$ и рассеивающие $\left(b\right)$ линзы и их условные обозначения.

В тонкой линзе главная оптическая ось пересекается в одной точке – оптическом центре линзы $O$. Световой луч проходит через оптический центр линзы, не отклоняясь от своего первоначального направления.

Тонкая линза имеет два главных фокуса, которые располагаются симметрично на главной оптической оси по отношению к линзе.

Пучки лучей, параллельные одной из всей совокупности побочных оптических осей, после прохождения через линзу тоже нацелены на точку $F\text{'}$, расположенную на пересечении побочной оси с фокальной плоскостью $Ф$.

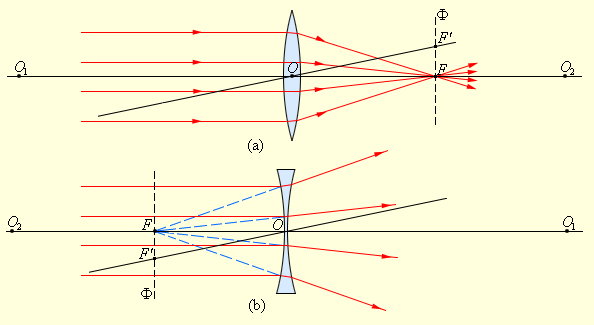
Рисунок $3.3.2.$ Преломление параллельного пучка лучей в собирающей $\left(a\right)$ и рассеивающей $\left(b\right)$ линзах. $O_1$ и $O_2$ – центры сферических поверхностей, $O_1{O}_2$ – главная оптическая ось, $О$ – оптический центр, $F$ – главный фокус, $F\text{'}$ – фокус, $OF\text{'}$ – побочная оптическая ось, $Ф$ – фокальная плоскость.

Главным свойством линз является способность передавать изображения предметов. Они, в свою очередь, бывают:

• Действительные и мнимые;
• Прямые и перевернутые;
• Увеличенные и уменьшенные.

Построение изображения в линзах

Геометрические построения помогают определить положение изображения, а также его характер. Для этой цели применяют свойства стандартных лучей, направление которых определено. Это лучи, которые проходят через оптический центр либо один из фокусов линзы, и лучи, параллельно расположенные главной либо одной из побочных оптических осей. Рисунки $3.3.3$ и $3.3.4$ демонстрируют данные построения.

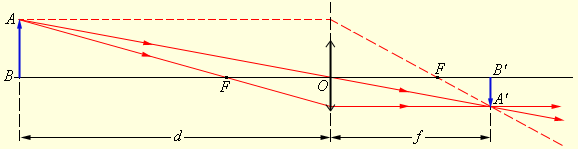
Рисунок $3.3.3.$ Построение изображения в собирающей линзе.

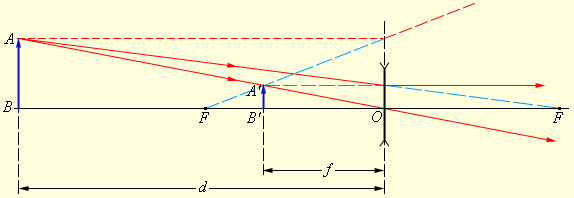
Рисунок $3.3.4.$ Построение изображения в рассеивающей линзе.

Стоит выделить то, что стандартные лучи, использованные на рисунках $3.3.3$ и $3.3.4$ для построения изображений, не проходят через линзу. Данные лучи не используются в построении изображения, но могут быть использованы в этом процессе.

Формула тонкой линзы аналогична формуле сферического зеркала. Можно вывести ее для параксиальных лучей из подобия треугольников на рисунках $3.3.3$ либо $3.3.4$.

Фокусное расстояние линз записывается с определенными знаками: собирающая линза $F>0$, рассеивающая $F<0$.

Величина $d$ и $f$ тоже подчиняются определенным знакам:

• $d>0$ и $f>0$ – применительно к действительным предметам (то есть реальным источникам света) и изображений;
• $d<0$ и $f<0$ – применительно к мнимым источникам и изображениям.

Для случая на рисунке $3.3.3$ $F>0$ (линза собирающая), $d=3F>0$ (действительный предмет).

Из формулы тонкой линзы получаем: $f=\frac{3}{2}F>0$, означает, что изображение действительное.

Для случая на рисунке $3.3.4$ $F<0$ (линза рассеивающая), $d=2\left|F\right|>0$ (действительный предмет), справедлива формула $f=-\frac{2}{3}F<0$, следовательно, изображение мнимое.

Линейные размеры изображения зависят от положения предмета по отношению к линзе.

Величину $h\text{'}$ удобно записывать со знаками плюс или минус, в зависимости от того, прямое оно или перевернутое. Она всегда положительна. Потому для прямых изображений применяется условие $\Gamma >0$, для перевернутых $\Gamma <0$. Из подобия треугольников на рисунках $3.3.3$ и $3.3.4$ нетрудно вывести формулу для расчета линейного увеличения тонкой линзы:

$Г=\frac{h\text{'}}{h}=-\frac{f}{d}$.

В примере с собирающей линзой на рисунке $3.3.3$ при $d=3F>0$, $f=\frac{3}{2}F>0$.

Значит,$\mathrm{ \; Г}=-\frac{1}{2}<0$ – изображение перевернутое и уменьшенное в два раза.

В примере с рассеивающей линзой на рисунке $3.3.4$ при $d=2\left|F\right|>0$, справедлива формула $f=-\frac{2}{3}\left|F\right|<0$; значит, $Г=\frac{1}{3}>0$ – изображение прямое и уменьшенное в три раза.

Оптическая сила $D$ линзы находится в зависимости от радиусов кривизны $R_1$ и $R_2$, ее сферических поверхностей, а также и от показателя преломления $n$ материала линзы. В теории оптики имеет место следующее выражение:

$D=\frac{1}{F}=(n-1)\left(\frac{1}{R_1}+\frac{1}{R_2}\right)$.

Выпуклая поверхность имеет положительный радиус кривизны, а вогнутая поверхность – отрицательным. Данная формула применима в изготовлении линз с заданной оптической силой.

Многие оптические приборы устроены таким образом, что свет последовательно проходит через $2$ или несколько линз. Изображение предмета от $1$-й линзы служит предметом (действительным или мнимым) для $2$-й линзы, выстраивающей, в свою очередь, $2$-е изображение предмета, которое также может быть действительным либо мнимым. Расчет оптической системы из $2$-х тонких линз состоит в
$2$-кратном применении формулы линзы, причем расстояние $d_2$ от $1$-го изображения до $2$-й линзы следует предложить равное величине $l–f_1$, где $l$ – это расстояние между линзами.

Вычисленная, по формуле линзы, величина $f_2$ предопределяет положение $2$-го изображения, а также его характер ($f_2>0$ – действительное изображение, $f_2<0$ – мнимое). Общее линейное увеличение $\Gamma$ системы из$\mathrm{ \; 2}$-х линз равняется произведению линейных увеличений $2$-х линз, то есть $\Gamma ={\Gamma }_1·{\Gamma }_2$. Если предмет либо его изображение находятся в бесконечности, тогда линейное увеличение не имеет смысла.

Астрономическая труба Кеплера и земная труба Галилея

Рассмотрим частный случай – телескопический ход лучей в системе из $2$-х линз, когда и предмет, и $2$-е изображение расположены на бесконечно больших расстояниях друг от друга. Телескопический ход лучей выполняется в зрительных трубах: земной трубе Галилея и астрономической трубе Кеплера.

Тонкая линза имеет некоторые недостатки, которые не позволяют получать изображения высокого разрешения.

Современные оптические приборы оснащены не тонкими линзами, а сложными линзовыми системами, в которых есть возможность исключить некоторые искажения.

В таких приборах, как фотоаппараты, проекторы и т.д., используются собирающие линзы для формирования действительных изображений предметов.

Что представляет собой фотоаппарат

Особенность работы фотоаппарата в том, что на плоской фотопленке получаются довольно резкие изображения предметов, которые находятся на различных расстояниях. Резкость меняется вследствие перемещения объектива относительно фотопленки. Изображения точек, которые не лежат в плоскости резкого наведения, выходят на снимках размытыми в виде рассеянных кружков. Размер $d$ данных кружков можно уменьшить методом диафрагмирования объектива, то есть уменьшения относительного отверстия $\frac{a}{F}$, как показано на рисунке $3.3.5$. Это в результате увеличивает глубину резкости.

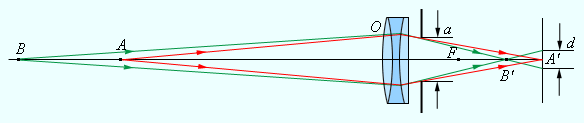
Рисунок $3.3.5.$ Фотоаппарат.

С помощью проекционного аппарата удается снять масштабные изображения. Объектив $O$ проектора фокусирует изображение плоского предмета (диапозитив $D$) на удаленном экране $Э$ (рисунок $3.3.6$). Система линз $K$ (конденсор) используется для концентрации света источника $S$ на диапозитиве. На экране воссоздается увеличенное перевернутое изображение. Масштаб проекционного устройства можно изменять, приближая или отдаляя экран и одновременно изменяя расстояние между диапозитивом $D$ и объективом $O$.

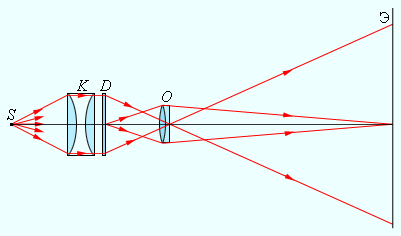
Рисунок $3.3.6.$ Проекционный аппарат.

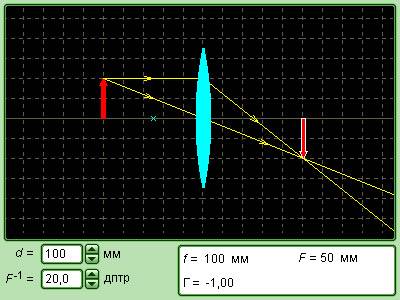
Рисунок $3.3.7.$ Модель тонкой линзы.

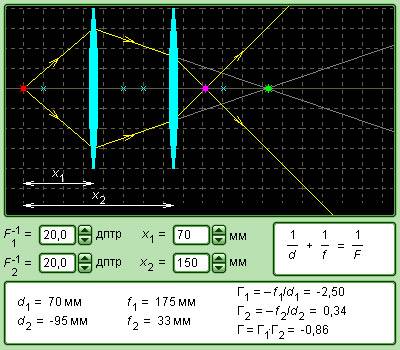
Рисунок $3.3.8.$ Модель системы из двух линз.