
Статью подготовили специалисты образовательного сервиса Zaochnik.
Квазистационарные процессы. RC- и RL-цепи
Содержание:
Колебательные и волновые процессы, которые изучаются в разных разделах физики, имеют много общих закономерностей. Движения груза на пружине, процессы в электрическом колебательном контуре, распространение света – все эти явления протекают аналогичным образом. Есть смысл говорить об их различной физической природе.
Для решения задачи о колебательных движениях груза на пружине необходимо знать и разбираться в законах Ньютона. Глубокие знания в электродинамике не требуются. Но математические уравнения, которые описывают эти состояния, одинаковые. Также обстоят дела и с волновыми процессами.
Квазистационарные процессы. Заряд и разряд конденсатора
Общность колебательных процессов и волновых закономерностей проявляется в общности математических уравнений, описывающих процессы различной физической природы.
Цепи постоянного тока распределяют электрический заряд на проводниках и токи на участках цепи стационарно, то есть независимо от времени. Электромагнитное поле таких цепей состоит из электростатического поля неподвижных зарядов и магнитного поля постоянных токов. Существование этих полей производится независимо друг от друга.
Если происходят изменения силы тока или напряжения на определенном участке цепи, то другие могут ощутить их на себе не сразу. Необходимо количество времени, равное времени распространения магнитного возмущения от одной точки к другой. Все электромагнитные возмущения обладают конечной скоростью, с которой и происходит их распространение. Она приравнивается к значению скорости света , тогда , где является расстоянием между наиболее удаленными точками цепи.
При наличии меньшего значения времени длительности процессов, происходящих в цепи, считается, что сила тока неизменна в любой момент времени на всех последовательно соединенных участках цепи. Такие процессы получили название квазистационарных.
Их исследуют при помощи законов постоянного тока, применяя к мгновенным значениям сил токов и напряжений на участках цепи.
Так как скорость света имеет достаточно большое значение, то установление электрического равновесия цепи достаточно мало. Отсюда следует, что квазистационарными считаются большинство процессов, протекающих очень быстро. Это сравнимо с колебаниями в радиотехнических цепях с многомиллионными частотами в секунду.
Простейшими примерами квазистационарных процессов являются процессы, проходящие в и цепях при подключении и отключении постоянного тока. Рисунок показывает электрическую цепь, которая состоит из конденсатора с емкостью , резистора с сопротивлением , источником тока с ЭДС, равняющейся .
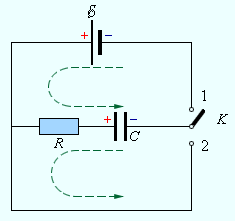
Рисунок Цепи зарядки и разрядки конденсатора через резистор.
Зарядка конденсатора через резистор
При замыкании ключа в положение конденсатор начнет заряжаться через резистор.
Квазистционарная цепь по закону Ома запишется как– это мгновенное значение силы тока в цепи, – мгновенное значение напряжения на конденсаторе. равняется изменению заряда конденсатора за единицу времени, то есть . В любой момент времени напряжение будет . Отсюда получаем, что: .
Это уравнение называется дифференциальным и описывает процесс заряжения конденсатора. При отсутствии первоначальной его зарядки, уравнение принимает вид:
, где выражение – постоянная времени цепи, которая состоит из резистора и конденсатора. Скорость процесса характеризуется величиной . При . На рисунке показан процесс зарядки конденсатора через резистор.
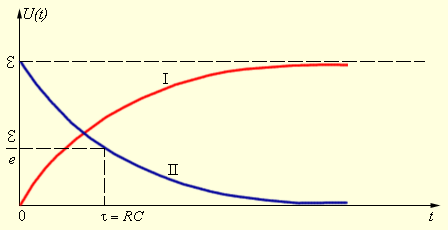
Рисунок Зарядка и разрядка конденсатора через резистор.
После полной зарядки конденсатора к напряжению необходимо переключить ключ в положение . Тогда пойдет процесс разряжения. Так как внешний источник цепи отсутствует, то . Разрядка описывается с помощью формулы
.
При разрежении, изображенном на рисунке , необходимо обратить внимание на зависимость . Если , тогда происходит уменьшение напряжения в конденсаторе в раз.
Также проходят процессы в цепи, если имеется индуктивность с резистором, имеющим сопротивление , как показано на рисунке
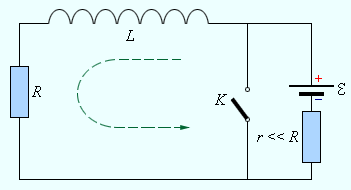
Рисунок Цепь, содержащая катушку с индуктивностью , резистор с сопротивлением и источник тока с ЭДС, равной .
Если цепь из рисунка замыкается ключом и внезапно размыкается, тогда можно говорить о процессе установления тока. Данная последовательная схема включает в себя источник тока и резистор с малым сопротивлением для того, чтобы с замкнутым ключом батарея не закоротила. Так как , для записи уравнения процесса установления тока с таким разрешено им пренебречь. Тогда .
Уравнение оказывается аналогичным уравнению, описывающему заряд конденсатора с переменной силой тока . Получаем:
, выражение – постоянная времени . Таким же образом получают закон убывания тока -цепей при замыкании ключа .
.
Видно, что процессы, происходящие в и цепях аналогичны механическим процессам во время движения в вязкой жидкости.
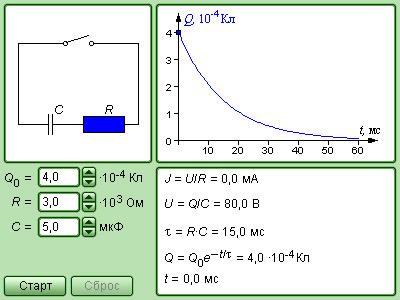
Рисунок Модель контура.
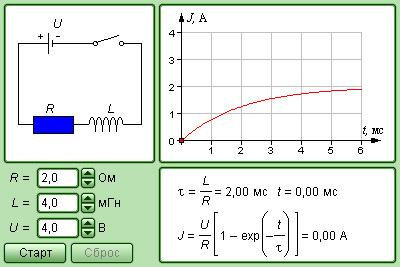
Рисунок Модель контура.
Навигация по статьям
