
Статью подготовили специалисты образовательного сервиса Zaochnik.
Последовательное и параллельное соединение проводников
Содержание:
Последовательное соединение проводников
Проводники в электрических цепях могут соединяться как последовательным, так и параллельным способами.
В условиях последовательного соединения проводников (рис. ) сила тока во всех проводниках одинакова:
.
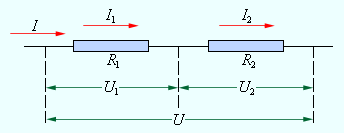
Рисунок Последовательное соединение проводников.
Опираясь на закон Ома, можно заявить, что напряжения и на проводниках равняются следующим выражениям:
.
Общее напряжение на обоих проводниках эквивалентно сумме напряжений и :
,
где является электрическим сопротивлением всей цепи.
Из этого следует, что общее сопротивление равняется сумме сопротивлений на входящих в данную цепь отдельных проводников:
.
Данный результат применим для любого количества последовательно соединенных проводников.
Параллельное соединение проводников
В условиях параллельного соединения (рис. ) напряжения и на обоих проводниках эквивалентны друг другу, из чего следует:
.
Совокупность существующих в обоих проводниках токов равняется значению тока в неразветвленной цепи, то есть:
.
Данный результат исходит из того, что заряды не могут копиться в точках разветвления, то есть в узлах и , цепи постоянного тока.
Так, например, узлу за время сообщается заряд , а уходит из узла за то же время заряд. Таким образом, подтверждается выражение .
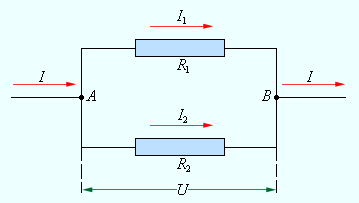
Рисунок Параллельное соединение проводников.
Опираясь на закон Ома, запишем для каждой ветви:
,
где является электрическим сопротивлением всей цепи, получим
В условиях параллельного соединения проводников обратная общему сопротивлению цепи величина, равняется сумме величин, обратных сопротивлениям параллельно включенных проводников.
Полученный вывод может быть применим для любого количества включенных параллельно проводников.
Применение формул для расчета сопротивления сложной цепи
Формулы для последовательного и параллельного соединений проводников дают возможность во многих случаях рассчитывать сопротивление сложной цепи, которая состоит из многих резисторов. На рис. проиллюстрирована подобная сложная цепь и указана последовательность необходимых для расчета вычислений.
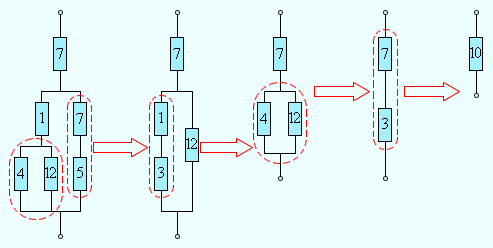
Рисунок Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны в омах
Стоит акцентировать внимание на том факте, что далеко не каждая сложная цепь, состоящая из проводников с разными сопротивлениями, может быть рассчитана с использованием формул для последовательного и параллельного соединений. На рис. изображена электрическая цепь, которую рассчитать данным методом не получится.
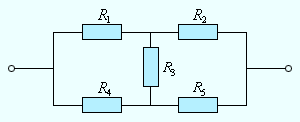
Рисунок Пример электрической цепи, не сводящейся к комбинации последовательно и параллельно соединенных проводников.
Аналогичные иллюстрированной на рисунке цепи, так же, как и цепи с разветвлениями, содержащие более одного источника, можно рассчитать, используя правила Кирхгофа.
Навигация по статьям
