
Статью подготовили специалисты образовательного сервиса Zaochnik.
Колебательный контур
Содержание:
Чаще всего в контур включают конденсатор определенной емкости, катушку индуктивности, сопротивление и источник сторонних ЭДС. На рисунке показана общая схема:
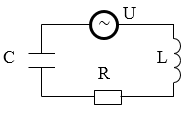
Рисунок
При особом соотношении элементов в контуре могут возникать колебания. Тогда такая система получает название колебательного контура.
Собственные колебания контура
Если системе в начальный момент времени сообщили определенное количество энергии, то она начинает совершать собственные колебания.
Важно, что постоянный источник ЭДС при этом отсутствует.
Если собственные колебания вызваны наличием только квазиупругой силы, то они являются гармоническими.
Возьмем для примера ситуацию, когда в колебательном контуре отсутствует источник ЭДС. В таком случае уравнение колебательного контура можно записать в следующем виде:
.
Решить уравнение можно, описав свободные колебания при сопротивлении, входящем в состав контура:
.
Здесь может быть указан косинус вместо синуса. В обоих случаях это будет верно, поскольку обе функции имеют соответствующий сдвиг. Если , то изменения заряда нельзя считать колебаниями. Если , то колебания в цепи становятся свободными. Если же и потери энергии на сопротивление незначительны, то такие колебания будут гармоническими.
Заряд конденсатора, изменения которого нельзя считать колебаниями, называется апериодическим.
Решение задач с колебательным контуром
Условие: дана схема цепи с конденсатором емкостью , резистором, сопротивление которого равно , и генератором тока , который формирует ток следующего вида:
при .
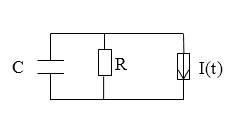
Рисунок
Запишите функцию данного конденсатора.
Решение
Для начала запишем формулу суммарного тока в цепи, воспользовавшись первым правилом Кирхгофа.
.
Здесь показателем обозначаются те токи, которые текут через конденсатор, преодолевая сопротивление, а – это ток, вырабатываемый генератором.
Поскольку на схеме указано параллельное соединение сопротивления и конденсатора, то запишем так:
.
Далее нам необходимы будут следующие формулы:
.
Подставим это значение в нужное уравнение и получим следующее:
.
Примем напряжение на конденсаторе равным нулю при в качестве изначального условия. Тогда установившееся на нем позже напряжение будет равно:
.
Решением уравнения станет запись следующего вида:
.
Ответ: .
Условие: дана схема электрической цепи. Сопротивление резистора на ней равно , емкость конденсатора – . Также в ней есть генератор постоянного напряжения. Сформулируйте зависимость напряжения на конденсаторе от времени после замыкания ключа при условии, что конденсатор не заряжен изначально.
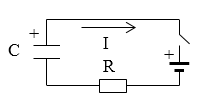
Рисунок
Решение
Зная второе правило Кирхгофа, мы можем записать следующее:
.
Здесь показатели выражают напряжение на сопротивлении и конденсаторе.
Также нам известно, что:
.
На рисунке мы видим последовательное соединение элементов цепи, значит:
.
Выбрав направление обхода контура и учитывая все нужные формулы, получим:
.
Вспомним начальные условия:
.
Следовательно, решением данного уравнения является функция .
Ответ: .
Навигация по статьям
