
Статью подготовили специалисты образовательного сервиса Zaochnik.
Уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой
Содержание:
В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.
Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.
Если плоскость проходит через заданную точку перпендикулярно к заданной прямой , то прямые, лежащие в этой плоскости, в том числе и проходящая через являются перпендикулярными заданной прямой .
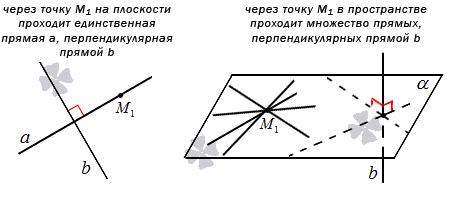
Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.
Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
Если на плоскости с системой координат имеем прямую , то ей соответствует уравнение прямой на плоскости, задается точка с координатами , а необходимо составить уравнение прямой , которая проходит через точку , причем перпендикулярно прямой .
По условию имеем координаты точки . Для написания уравнения прямой необходимо иметь координаты направляющего вектора прямой , или координаты нормального вектора прямой , или угловой коэффициент прямой .
Необходимо получить данные из заданного уравнения прямой . По условию прямые и перпендикулярные, значит, направляющий вектор прямой считается нормальным вектором прямой . Отсюда получим, что угловые коэффициенты обозначаются как и . Они связаны при помощи соотношения .
Получили, что направляющий вектор прямой имеет вид , отсюда нормальный вектор - , где значения . Тогда запишем общее уравнение прямой, проходящее через точку с координатами , имеющее нормальный вектор , имеющее вид .
Нормальный вектор прямой определен и имеет вид , тогда направляющий вектор прямой является вектором , где значения . Значит осталось составить каноническое или параметрическое уравнение прямой , проходящее через точку с координатами с направляющим вектором , имеющее вид или соответственно.
После нахождения углового коэффициента прямой можно высчитать угловой коэффициент прямой . Он будет равен . Отсюда следует, что можно записать уравнение прямой , проходящей через с угловым коэффициентом в виде .
Полученное уравнение прямой, проходящее через заданную точку плоскости перпендикулярно заданной. Если того требуют обстоятельства, можно переходить к другому виду данного уравнения.
Решение примеров
Рассмотрим составление уравнения прямой, проходящей через заданную точку плоскости и перпендикулярно заданной прямой.
Записать уравнение прямой а, которая проходит через точку с координатами и перпендикулярна прямой , которое задано каноническим уравнением прямой .
Решение
Из условия имеем, что является направляющим вектором прямой . Координаты вектора являются координатами нормального вектора прямой , так как прямые и взаимно перпендикулярны. Значит, получаем . Теперь необходимо записать уравнение прямой, проходящее через точку , имеющее нормальный вектор с координатами .
Получим уравнение вида:
Полученное уравнение является искомым.
Ответ: .
Составить уравнение прямой, которая проходит через начало координат системы координат , перпендикулярно прямой .
Решение
Имеем, что является нормальным вектором заданной прямой. Отсюда - координаты искомого направляющего вектора прямой.
Зафиксируем уравнение прямой, проходящую через начало координат с направляющим вектором . Получим, что . Полученное выражение является уравнение прямой, проходящей через начало координат перпендикулярно прямой .
Ответ: .
Записать уравнение прямой, проходящей через точку с координатами перпендикулярно прямой .
Решение
Из уравнения угловой коэффициент имеет значение . Угловой коэффициент прямой, которая перпендикулярна ей имеет значение . Отсюда делаем вывод, что прямая, проходящая через точку с координатами перпендикулярно прямой , равна .
Ответ: .
Навигация по статьям
