
Статью подготовили специалисты образовательного сервиса Zaochnik.
Координаты точки пересечения прямой и плоскости - примеры нахождения
Содержание:
Данная глава рассказывает о том, как найти координаты точки пересечения прямой с плоскостью при заданных уравнениях, определяющих эту плоскость. Будет рассмотрено понятие точки пересечения прямой с плоскостью, два способа нахождения координат точки пересечения прямой с плоскостью.
Точка пересечения прямой и плоскости – определение
Для углубленного изучения теории необходимо начать рассмотрение с понятия точки, прямой, плоскости. Понятие о точке, прямой линии рассматривается как на плоскости, так и в пространстве. Для детального рассмотрения необходимо обратиться к теме о прямой и плоскости в пространстве.
Существует несколько вариаций расположения прямой относительно плоскости и пространства:
- прямая лежит в плоскости;
- прямая параллельна плоскости;
- прямая пересекает плоскость.
Если рассмотреть третий случай, то отчетливо видно, что прямая с плоскостью при пересечении образуют общую точку, которую называют точкой пересечения прямой и плоскости. рассмотрим данный случай на примере.
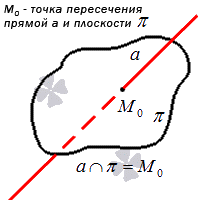
Нахождение координат точки пересечения прямой и плоскости
Была введена прямоугольная система координат трехмерного пространства. Каждая прямая имеет свое собственное уравнение, а каждая плоскость соответствует своему заданному уравнению, каждая точка имеет определенное количество действительных чисел – координат.
Чтобы подробно разобраться в теме координат пересечения, необходимо знать все виды уравнения прямой в пространстве и уравнений плоскости. в данном случае пригодятся знания о переходе от одного вида уравнения к другому.
Рассмотрим задачу, которая основывается на заданном пересечении прямой и плоскости. она сводится к нахождению координат пересечений.
Вычислить, может ли точка с координатами являться точкой пересечения прямой с плоскостью .
Решение
Когда точка принадлежит некоторой прямой, координаты точки пересечения являются решением обоих уравнения. Из определения имеем, что при пересечении образуется общая точка. Для решения задания необходимо подставить в оба уравнения координаты точки и вычислить. Если она является точкой пересечения, то оба уравнения будут соответствовать.
Представим координаты точки и получим:
Так как получаем верные равенства, делаем вывод, что точка - точка пересечения заданной прямой с плоскостью.
Ответ: заданная точка с координатами является точкой пересечения.
Если координаты точки пересечения являются решением обоих уравнений, то они пересекаются.
Первый способ нахождения координат пересечения прямой и плоскости.
Когда задается прямая с плоскостью прямоугольной системы координат, известно, что они пересекаются в точке . Для начала займемся поиском координат заданной точки пересечения при заданном уравнении плоскости, имеющего вид с прямой линией , являющейся пересечением плоскостей и . Данный способ задания прямой в пространстве рассматривается в статье уравнения прямой и уравнения двух пересекающихся плоскостей.
Необходимые нам координаты прямой и плоскости должны удовлетворять обоим уравнениям. Таким образом задается система линейных уравнений, имеющая вид
Решение системы подразумевает обращение каждого тождества в верное равенство. Следует отметить, что при таком решении мы определяем координаты пересечения плоскостей вида . Для закрепления материала рассмотрим решение данных задач.
Прямая задана уравнением двух пересекающихся плоскостей , причем пересекает еще одну . Необходимо найти координаты точки пересечения.
Решение
Необходимые координаты получим при составлении и решении системы, имеющей вид .
Следует обратить внимание на тему решения систем линейных уравнений.
Возьмем систему уравнений вида и произведем вычисления по определителю основной матрицы системы. Получаем, что
Так как определитель матрицы не равен нулю, система имеет только одно решение. Для этого мы применим метод Крамера. Он считается очень удобным и подходящим для данного случая.
Отсюда следует, что координаты точки пересечения заданной прямой и плоскости имеет значение .
Ответ: .
Система уравнений вида имеет одно единственное решение. Когда прямая определена такими уравнениями, как , а плоскость задается уравнением , то они пересекаются. Когда прямая лежит в плоскости, система выдает бесконечное множество решений. При их параллельности уравнение решений не имеет, так как нет общих точек пересечения.
Найти точку пересечения прямой и плоскости .
Решение
Заданные уравнения необходимо преобразовать в систему . Когда она будет иметь единственное решение, то получим искомые координаты пересечения в точке. При условии, если нет решений, то они параллельны, либо прямая лежит в этой же плоскости.
Получим, что основная матрица системы – , расширенная – . Нам необходимо определить ранг матрицы и методом Гаусса:
Тогда получим, что ранг основной матрицы равен рангу расширенной. Применим теорему Кронекера-Капелли, отсюда видно, что у системы есть бесконечное множество решений. Получим, что прямая принадлежит плоскости , что говорит об их невозможности пересечения и наличии общей точки.
Ответ: нет координат точки пересечения.
Задано пересечение прямой и плоскости , найти координаты точки пересечения.
Решение
Необходимо собрать заданные уравнения в систему вида . Для решения применяем метод Гаусса. С его помощью мы определим все имеющиеся решения коротким путем. Для этого запишем
Применив метод Гауса, стало понятно, что равенство неверное, так как система уравнений решений не имеет.
Делаем вывод, что прямая с плоскостью не имеют пересечений. Отсюда следует, что невозможно найти координаты точки, так как они не пересекаются.
Ответ: нет точек пересечения, так как прямая параллельна плоскости.
Когда прямая имеет задана параметрическим или каноническим уравнением, то отсюда можно найти уравнение пересекающихся плоскостей, которые определяют прямую , после чего искать необходимые координаты точки пересечений. Имеется еще один метод, который применяется для нахождения координат точки пересечения прямой и плоскости.
Второй способ нахождения точки начинается с задания прямой , пересекающей плоскость в точке . Необходимо найти координаты заданной точки пересечения при заданном уравнении плоскости . Прямую а определяем параметрическими уравнениями, имеющими вид .
Когда в уравнение производится подстановка , выражение примет вид уравнения с неизвестной . Необходимо разрешить его относительно, тогда получим , которое соответствует координатам точки, в которой они пересекаются. Вычисление координат точки производится из .
Подробнее этот способ будет рассмотрен на примерах, приведенных ниже.
Найти координаты точки пересечения прямой с плоскостью .
Решение
Для решения системы, необходимо произвести подстановку. Тогда получаем, что
Найдем координаты точки пересечения плоскости с прямой, используя параметрические уравнения, со значением .
Получим :
Ответ: .
Когда прямая вида принадлежит плоскости , тогда необходимо подставить туда уравнение плоскости выражения , тогда получим тождество такого вида . При параллельности плоскости и прямой получаем неверное равенство, так как нет точек пересечения.
Если прямая задана каноническим уравнением, имеющим вид , тогда необходимо переходить от канонических к параметрическим при поиске координат точки пересечения прямой с плоскостью , то есть получим и применим необходимы способ для нахождения координат точки пересечения заданной прямой и плоскости в пространстве.
Навигация по статьям
