
Статью подготовили специалисты образовательного сервиса Zaochnik.
Непосредственное вычисление пределов, таблица пределов функций
Содержание:
Определение непрерывности функции в точке и передела функции на бесконечности и на использовании свойств предела непрерывной функции способствует непосредственному вычислению пределов.
Значение предела в точке непрерывности определено значением функции в этой точке.
При опоре на свойства основные элементарные функции имеют предел в любой точке из области определения, вычисляется как значение соответствующей функции в этих точках.
Произвести вычисление предела функции
Решение
Функция арктангенса отличается непрерывностью на всей своей области определения. Отсюда получим, что в точке функция является непрерывной. Из определения имеем, что для нахождения предела является значением этой же функции. Тогда необходимо произвести подстановку. Получим, что
Ответ:
Для вычисления односторонних пределов необходимо использовать значения точек границ предела. У акрксинуса и акрккосинуса имеются такие значения или .
При или вычисляются пределы функции, заданные на бесконечностях.
Для упрощения выражений применяют свойства пределов:
- , является коэффициентом.
- , применяемое при получении неопределенности предела.
- ,используемое для непрерывных функций, где знак функции и предельного перехода можно менять местами.
Для того, чтобы научиться вычислять переделы, необходимо знать и разбираться в основных элементарных функциях. Ниже приведена таблица, в которой имеются переделы этих функций с приведенными разъяснениями и подробным решением. Для вычисления необходимо основываться на определении предела функции в точке и на бесконечности.
Таблица пределов функции
Для упрощения и решения пределов используется данная таблица основных пределов.
|
Функция корень n-ой степени , где Для любых из опрелеления |
Функция корень n-ой степени , где
|
|
Степенная функция
|
Степенная функция
|
|
Показательная функия
Для любых из области опреления |
Показательная функия
Для любых знвчений из област опредения |
|
Логарифмическая функция Для любых из области опрелеления |
Логарифмическая функция Для любых из области опрелеления |
|
Тригонометрические функции
не существует Для любых из области опрелеления |
Тригонометрические функции
не существует Для любых из области опрелеления |
|
Обратные тригонометрические функции
Для любых из области опрелеления
Для любых из области опрелеления |
Обратные тригонометрические функции
Для любых из области опрелеления
Для любых из области опрелеления |
Произвести вычисление предела .
Решение
Для решения необходимо подставить значение . Получаем, что
Ответ:
Произвести вычисление предела функции
Решение
Для того, чтобы раскрыть предел, необходимо подставить значение х, к которому стремится предел функции. В данном случае нужно произвести подстановку . Подставляем числовое значение и получаем:
Предел записывается в виде . Далее необходимо заняться значением показателя. Он является степенной функцией . В таблице пределов, предоставленной выше, имеем, что и , значит, имеем право записать как
Теперь вычислим предел. Получит вид
По таблице пределов с показательными функциями, имеющими основание больше получаем, что
Ответ:
Когда задан более сложный предел, то при помощи таблицы не всегда получится получать целое или конкретное значение. Чаще получаются разные виды неопределенностей, для разрешения которых необходимо применять правила.
Рассмотрим графическое разъяснение приведенной выше таблицы пределов основных элементарных функций.
Предел константы
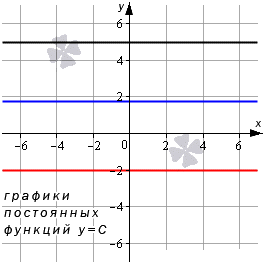
Из рисунка видно, что функция имеет предел на бесконечности. Такой же предел при аргументе, который стремится к . Он равняется числу .
Предел функции корень n-ой степени
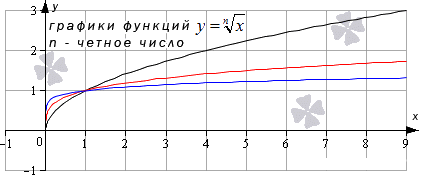
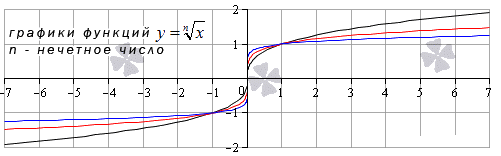
Четные показатели корня применимы для , а нечетные, равные больше, чем значение , – для . Область определения может принимать абсолютно любое значение х предела заданной функции корня -ой степени, равного значению функции в заданной точке.
Предел степенной функции
Необходимо разделить все степенные функции по группам, где имеются одинаковые значения пределов, исходя из показателя степени.
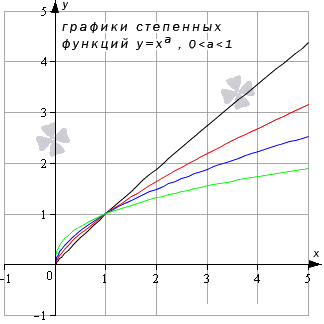
- Когда является положительным числом, тогда и . Когда принимает любое значение, тогда предел степенной функции равняется значению функции в точке. Иначе это записывается как .
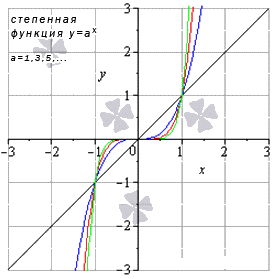
- Когда является положительным четным числом, тогда получаем и , причем из данной области определения является пределом степенной функции и равняется значением функции в этой точке. Предел имеет вид .
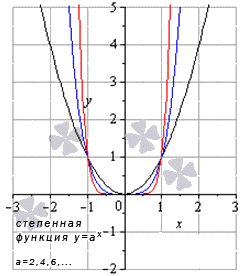
- Когда имеет другие значения, тогда , а область определения способствует определению предела функции в заданной точке.
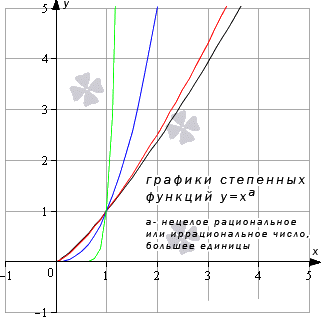
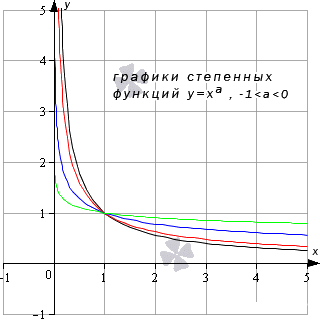
- Когда имеет значение отрицательных чисел, тогда получаем , а значения может быть любым из заданной области определения и равняется функции в заданной точке. Получаем, что и.
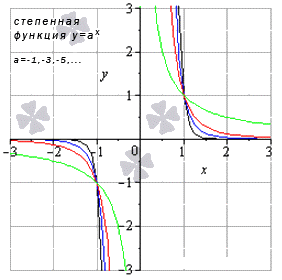
- Когда является отрицательным четным числом, тогда получаем , а любое значение на области определения дает результат предела степенной функции равным значению функции в точке. Запишем как и .
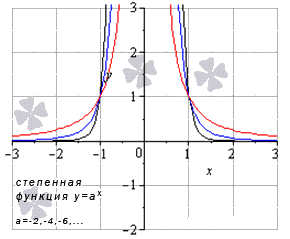
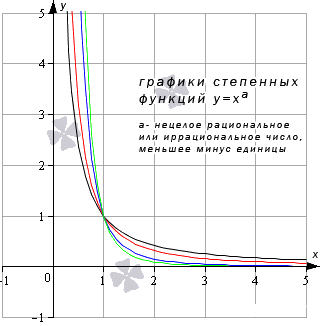
- Когда значение имеет другие действительные отрицательные числа, тогда получим и , когда принимает любое значение из своей области определения, тогда предел степенной функции равняется значению функции в этой точке.
Предел показательной функции
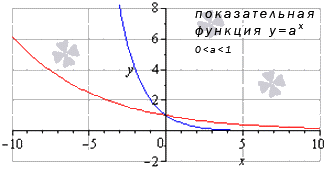
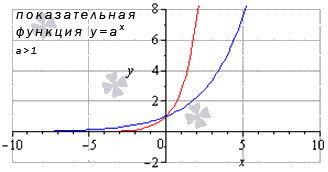
Когда , имеем, что , любое значение из области определения дает пределу показательной функции значению функции в точке.
Когда , тогда , а любое значение из области определения дает предел функции равный значению этой функции в точке.
Предел логарифмической функции
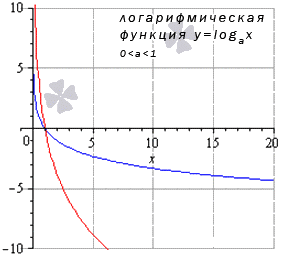
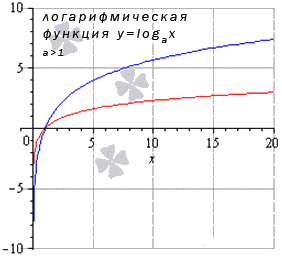
Когда имеем , тогда , для всех остальных значений из заданной области определения предел показательной функции равняется значению заданной функции в точках.
Когда , получаем ,остальные значения в заданной области определения дают решение предела показательной функции равному ее значению в точках.
Предел тригонометрических функций
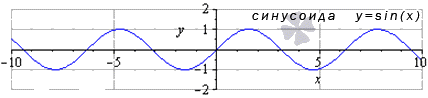
Предел бесконечности не существует для таких функций как . Любое значение , входящее в область определения, равняется значению функции в точке.
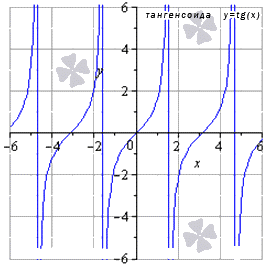
Функция тангенса имеет предел вида или , тогда остальные значения , принадлежащие области определения тангенса, равняется значению функции в этих точках.
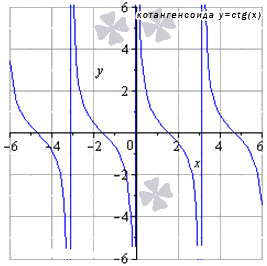
Для функции получаем или , тогда остальные значения , принадлежащие области определения, дают предел котангенса, равный значению функции в этих точках.
Предел обратных тригонометрических функций
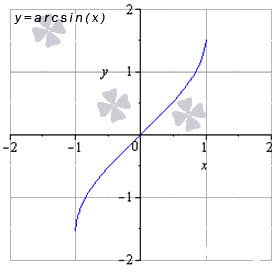
Функция арксинус имеет предел вида и , остальные значения из области определения равняются значению функции в заданной точке.
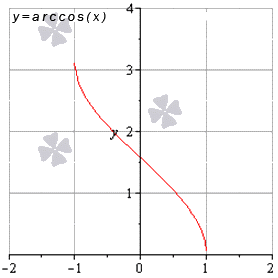
Функция арккосинус имеет предел вида и , когда остальные значения , принадлежащие области определения, имеют предел арккосинуса, равного значению функции в этой точке.
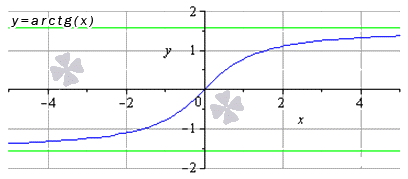
Функция арктангенс имеет предел вида и , причем другие значения , входящие в область определения, равняется значению функции в имеющихся точках.
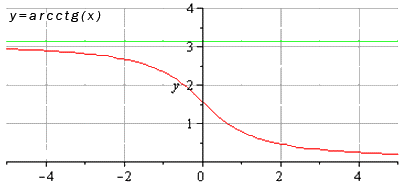
Функция котангенса имеет предел вида и , где принимает любое значение из своей заданной области определения, где получаем предел арккотангенса, равного значению функции в имеющихся точках.
Все имеющееся значения пределов применяются в решении для нахождения предела любой из элементарных функций.
Навигация по статьям
