
Статью подготовили специалисты образовательного сервиса Zaochnik.
Предел функции: основные понятия и определения
Содержание:
В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.
Понятие предела
В математике принципиально важным является понятие бесконечности, обозначаемое символом . Его следует понимать как бесконечно большое или бесконечно малое число. Когда мы говорим о бесконечности, часто мы имеем в виду сразу оба этих ее смысла, однако запись вида или не стоит заменять просто на .
Запись предела функции имеет вид . В нижней части мы пишем основной аргумент , а с помощью стрелочки указываем, к какому именно значению он будет стремиться. Если значение является конкретным действительным числом, то мы имеем дело с пределом функции в точке. Если же значение стремится к бесконечности (не важно, или ), то следует говорить о пределе функции на бесконечности.
Предел бывает конечным и бесконечным. Если он равен конкретному действительному числу, т.е. , то его называют конечным пределом, если же или , то бесконечным.
Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.
Что такое предел функции
В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.
Число является пределом функции при , если последовательность ее значений будет сходиться к для любой бесконечно большой последовательности аргументов (отрицательной или положительной).
Запись предела функции выглядит так: .
При предел функции является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).
Запись выглядит как .
Докажите равенство с помощью основного определения предела для .
Решение
Начнем с записи последовательности значений функции для бесконечно большой положительной последовательности значений аргумента .
Мы видим, что значения будут постепенно уменьшаться, стремясь к . См. на картинке:
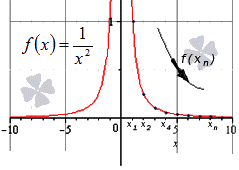
Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.
Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:
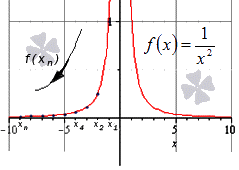
Ответ: Верность данного в условии равенства подтверждена.
Вычислите предел .
Решение
Начнем, как и раньше, с записи последовательностей значений для бесконечно большой положительной последовательности аргументов. Например, .
Мы видим, что данная последовательность бесконечно положительна, значит,
Переходим к записи значений бесконечно большой отрицательной последовательности, например, .
Поскольку она тоже стремится к нулю, то .
Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными – отрицательных.
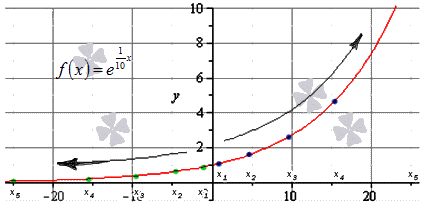
Ответ: .
Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.
Число является пределом функции слева при в том случае, когда последовательность ее значений сходится к данному числу при любой последовательности аргументов функции , сходящейся к , если при этом ее значения остаются меньше ().
Такой предел на письме обозначается как .
Теперь сформулируем, что такое предел функции справа.
Число является пределом функции справа при в том случае, когда последовательность ее значений сходится к данному числу при любой последовательности аргументов функции , сходящейся к , если при этом ее значения остаются больше ().
Этот предел мы записываем как .
Мы можем найти предел функции в некоторой точке тогда, когда для нее существуют равные пределы с левой и правой стороны, т.е. . В случае бесконечности обоих пределов предел функции в исходной точке также будет бесконечен.
Теперь мы разъясним данные определения, записав решение конкретной задачи.
Докажите, что существует конечный предел функции в точке и вычислите его значение.
Решение
Для того чтобы решить задачу, нам потребуется вспомнить определение предела функции в точке. Для начала докажем, что у исходной функции имеется предел слева. Запишем последовательность значений фукнции, которая будет сходиться к , если :
Поскольку приведенная последовательность сводится к , мы можем записать, что .
Далее докажем наличие предела справа: запишем аргументы в последовательности, которая будет сходиться к , если :
Значения функции в этой последовательности будут выглядеть так:
Данная последовательность также сходится к , значит, .
Мы получили, что пределы с правой и левой стороны у данной функции будут равными, значит, предел функции в точке существует, и .
Вы можете увидеть ход решения на иллюстрации (зеленые точки– последовательность значений, сходящаяся к , синие – к ).
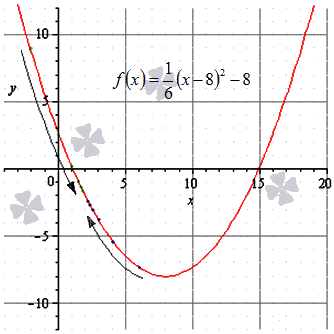
Ответ: Пределы с правой и левой стороны у данной функции будут равными, значит, предел функции существует, и .
Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.
Навигация по статьям
