
Статью подготовили специалисты образовательного сервиса Zaochnik.
Работа в электрическом поле. Потенциал
Содержание:
Работа сил электростатического поля. Понятие потенциала
Когда пробный заряд перемещается в электрическом поле, можно говорить о работе, совершаемой в данный момент электрическими силами. Для малого перемещения формулу работы можно записать так: .
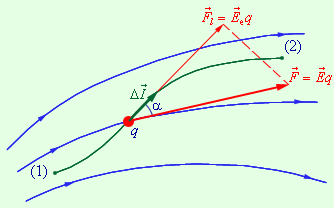
Рисунок . Малое перемещение заряда и работа, совершаемая в данный момент электрическими силами.
Теперь посмотрим, какую работу по перемещению заряда совершают силы в электрическом поле, которое создается распределенным зарядом, не изменяющимся во времени. Такое поле еще называют электростатическим. У него есть важное свойство, о котором мы поговорим в этой статье.
При перемещении заряда из одной точки электростатического поля в другую работа сил электрического поля будет зависеть только от величины этого заряда и положением начальной и конечной точки в пространстве. Форма траектории при этом не имеет значения.
У гравитационного поля есть точно такое же свойство, что неудивительно, поскольку соотношения, с помощью которых мы описываем кулоновские и гравитационные силы, одинаковы.
Исходя из того, что форма траектории не имеет значения, мы можем также сформулировать следующее утверждение:
Когда заряд в электростатическом поле перемещается по любой замкнутой траектории, работа сил поля равна . Поле, обладающее таким свойством, называется консервативным, или потенциальным.
Ниже приведена иллюстрация силовых линий в кулоновском поле, образованных точечным зарядом , а также две траектории перемещения пробного заряда в другую точку. Символом на одной из траекторий обозначается малое перемещение. Запишем формулу работы кулоновских сил на нем:
.
Следовательно, зависимость существует только между работой и расстоянием между зарядами, а также их изменением . Проинтегрируем данное выражение на интервале от до и получим следующее:
.
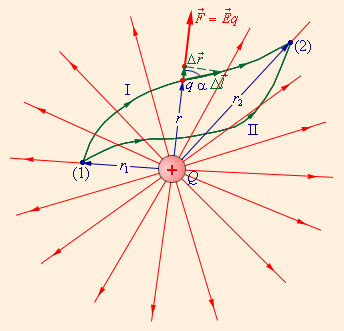
Рисунок Траектории перемещения заряда и работа кулоновских сил. Зависимость от расстояния между начальной и конечной точкой траектории.
Результат применения данной формулы не будет зависеть от траектории. Для двух различных траекторий перемещения заряда, указанных на изображении, работы кулоновских сил будут равны. Если же мы изменим направление на противоположное, то и работа также поменяет знак. А если траектории будут соединены, т.е. заряд будет перемещаться по замкнутой траектории, то работа кулоновских сил будет нулевой.
Вспомним, как именно создается электростатическое поле. Оно представляет собой сочетание точечных разрядов. Значит, согласно принципу суперпозиции, работа результирующего поля, совершаемая при перемещении пробного заряда, будет равна сумме работ кулоновских полей тех зарядов, из которых состоит электростатическое поле. Соответственно, величина работы каждого заряда не будет зависеть от того, какой формы траектория. Значит, и полная работа не будет зависеть от пути – важно лишь местоположение начальной и конечной точки.
Поскольку у электростатического поля есть свойство потенциальности, мы можем добавить новое понятие – потенциальная энергия заряда в электрическом поле. Выберем какую-либо точку, поместим в нее разряд и примем его потенциальную энергию за .
Потенциальная энергия заряда, помещенного в любую точку пространства относительно нулевой точки, будет равна той работе, которая совершается электростатическим полем при перемещении заряда из этой точки в нулевую.
Обозначив энергию как , а работу, совершаемую зарядом, как , запишем следующую формулу:
.
Обратите внимание, что энергия обозначается именно буквой , а не , поскольку в электростатике – это напряженность поля.
Потенциальная энергия электрического поля является определенной величиной, которая зависит от выбора точки отсчета (нулевой точки). На первый взгляд в таком определении есть заметная неоднозначность, однако на практике она, как правило, не вызывает недоразумений, поскольку сама по себе потенциальная энергия физического смысла не имеет. Важна лишь разность ее значений в начальной и конечной точке пространства.
Чтобы вычислить работу, которая совершается электростатическим полем при перемещении точечного заряда из точки в точку , нужно найти разность значений потенциальной энергии в них. Путь перемещения и выбор нулевой точки значения при этом не имеют.
.
Если мы поместим заряд в электростатическое поле, то его потенциальная энергия будет прямо пропорциональна его величине.
Понятие потенциала электрического поля
Потенциал электрического поля – это физическая величина, значение которой можно найти, разделив величину потенциальной энергии электрического заряда в электростатическом поле на величину этого заряда.
Он обозначается буквой . Это важная энергетическая характеристика электростатического поля.
.
Если мы умножим величину заряда на разность потенциалов начальной и конечной точки перемещения, то мы получим работу, совершаемую при этом перемещении.
.
Потенциал электрического поля измеряется в вольтах .
.
Разность потенциалов в формулах обычно обозначается .
Чаще всего при решении задач на электростатику в качестве нулевой берется некая бесконечно удаленная точка. Учитывая это, мы можем переформулировать определение потенциала так:
Потенциал электростатического поля точечного заряда в некоторой точке пространства будет равен той работе, которая совершается электрическими силами тогда, когда единичный положительный заряд удаляется из этой точки в бесконечность.
.
Чтобы вычислить потенциал точечного заряда на расстоянии , на котором размещается бесконечно удаленная точка, нужно использовать следующую формулу:
С помощью нее мы также можем найти потенциал поля однородно заряженной сферы или шара при , что следует из теоремы Гаусса.
Изображение электрических полей с помощью эквипотенциальных поверхностей
Чтобы наглядно изобразить электростатические поля, кроме силовых линий используются поверхности, называемые эквипотенциальными.
Эквипотенциальная поверхность (поверхность равного потенциала) – это такая поверхность, у которой во всех точкам потенциал электрического поля одинаков.
Эквипотенциальные поверхности и силовые линии на изображении всегда находятся перпендикулярно друг другу.
Если мы имеем дело с точечным зарядом в кулоновском поле, то эквипотенциальные поверхности в данном случае являются концентрическими сферами. На изображениях ниже показаны простые электростатические поля.
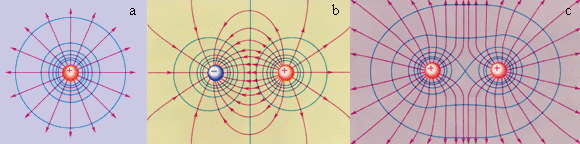
Рисунок Красным показаны силовые линии, а синим – эквипотенциальные поверхности простого электрического поля. На первом рисунке изображен точечный заряд, на втором –электрический диполь, на третьем – два равных положительных заряда.
Если поле однородное, то его эквипотенциальные поверхности являются параллельными плоскостями.
В случае малого перемещения пробного заряда вдоль силовой линии из начальной точки в конечную точку мы можем записать такую формулу:
,
где – изменение потенциала. Отсюда выводится, что:
или .
Это соотношение передает связь между потенциалом поля и его напряженностью. Буквой обозначена координата, которую следует отсчитывать вдоль силовой линии.
Зная принцип суперпозиции напряженности полей, которые создаются электрическими разрядами, мы можем вывести принцип суперпозиции для потенциалов:
Навигация по статьям
