
Статью подготовили специалисты образовательного сервиса Zaochnik.
Вектор напряженности электрического поля
Содержание:
По теории близкодействия взаимодействия между заряженными телами, удаленными друг от друга, происходит с помощью электромагнитных полей, создаваемых этими телами в окружающем их пространстве. Если поле было создано неподвижными частицами, то его относят к электростатическому. Когда происходят изменения во времени, получает название стационарного. Электростатическое поле является стационарным. Оно считается частным случаем электромагнитного поля.
Характеристика электрического поля
Силовая характеристика электрического поля – вектор напряженности, который можно найти по формуле:
, где - сила, действующая со стороны поля на неподвижный (пробный) заряд . Его значение должно быть настолько мало, чтобы отсутствовала возможность искажать поле, напряженность которого с его помощью и измеряют. По уравнению видно, что напряженность совпадает по направлению с силой, с которой поле действует на единичный положительный пробный заряд.
У напряженности электростатического поля нет зависимости от времени. Когда она во всех точках поля одинакова, тогда поле называют однородным. В другом случае – неоднородным.
Силовые линии
Чтобы изобразить электростатические поля графически, необходимо задействовать понятие силовых линий.
Силовые линии – это линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках.
Такие линии в электростатическом поле разомкнутые. Они начинаются на положительных зарядах и заканчивают на отрицательных. Реже уходят в бесконечность или возвращаются из нее. Силовые линии поля не могу пересекаться.
Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно:
.
Результирующий вектор напряженности сводится к нахождению векторной суммы напряженностей, составляющих его «отдельные» поля. При распределении непрерывного заряда, поиск суммарной напряженности поля производится по формуле:
.
Интегрирование проводится по области распределения зарядов. Если их распределение идет по линии ( - линейная плотность распределения заряда), то интегрирование тоже. Когда распределение зарядов идет по поверхности и поверхностная плоскость обозначается как , тогда интегрируют по поверхности.
Интегрирование по объему выполняется, если имеется объемное распределение заряда:
, где - объемная плотность распределения заряда.
Что называется напряженностью электрического поля
Напряженность поля в диэлектрике равняется векторной сумме напряженностей полей, которые создают свободные и связанные заряды:
.
Зачастую бывают случаи, когда диэлектрик изотропный. Тогда запись напряженности поля имеет вид:
, где обозначает относительную диэлектрическую проницаемость среды в рассматриваемой точке поля.
Отсюда следует, что по выражению имеется однородный изотропный диэлектрик с напряженностью электрического поля в меньше, чем в вакууме.
Напряженность электростатического поля системы точечных зарядов равняется:
.
В системе СГС напряженность поля точечного заряда в вакууме:
.
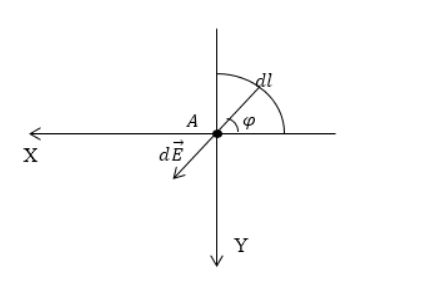
Дан равномерно распределенный заряд по четверти окружности радиуса с линейной плотностью . Необходимо найти напряженность поля в точке , являющейся центром окружности.
Решение
Рисунок
Произведем выделение на заряженной части окружности элементарного участка , который будет создавать элемент поля в точке . Следует записать выражение для напряженности, то есть для . Тогда формула примет вид:
.
Проекция вектора на ось составит:
.
Произведем выражение через линейную плотность заряда :
.
Необходимо использовать для преобразования :
,
где .
Далее перейдем к нахождению полной проекции при помощи интегрирования ,
по с изменением угла .
.
Перейдем к проекции вектора напряженности на :
.
Следует проинтегрировать с изменяющимся углом :
.
Произведем нахождение модуля вектора напряженности в точке , применив теорему Пифагора:
.
Ответ: .
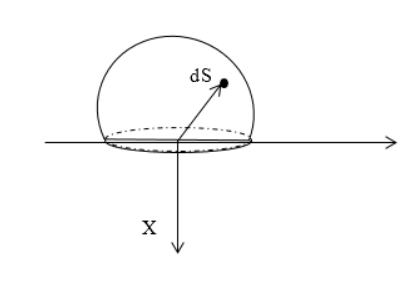
Найти напряженность электростатического поля равномерно заряженной полусферы с радиусом . Поверхностная плотность заряда равняется .
Решение
Рисунок
Следует выделить на поверхности заряженной сферы элементарный заряд , располагаемый на элементе площади . Запись, используя сферические координаты , равняется:
,
при .
Элементарная напряженность поля точечного заряда в системе :
.
Необходимо спроецировать вектор напряженности на :
.
Произведем выражение заряда через поверхностную плотность заряда:
.
Подставим в , используя , проинтегрируем и запишем:
.
Тогда .
Отсюда следует, что .
Ответ: напряженность полусферы в центре равняется .
Навигация по статьям
