
Статью подготовили специалисты образовательного сервиса Zaochnik.
Поляризация света
Содержание:
Начало XIX века для физики ознаменовалось развитием волновой теории света, которым занимались ученые Т. Юнг и О. Френель. В то время природа световых волн оставалась неизвестной. Изначально предполагалось, что свет является распространяющимися в некоторой гипотетической среде – эфире продольными волнами. Однако в процессе изучения явлений дифракции и интерференции вопрос о том, продольные или поперечные световые волны, стал второстепенен. На тот момент казалось невозможным, что свет – это поперечные волны, по той причине, что по аналогии с механическими волнами пришлось бы признать эфир твердым телом, ведь поперечные механические волны не обладают возможностью распространяться в газообразной или же жидкой среде.
Несмотря ни на что, постепенно копились свидетельствующие в пользу поперечности световых волн экспериментально полученные факты.
Еще в конце XVII века было обнаружено, что кристалл исландского шпата обладает свойством, позволяющим ему раздваивать проходящие сквозь него лучи. Данное явление было названо двойным лучепреломлением (рис. ).
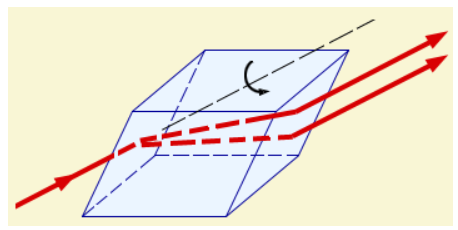
Рисунок Прохождение света через кристалл исландского шпата (двойное лучепреломление). При повороте кристалла относительно направления первоначального луча оба луча, которые проходят через кристалл, тоже поворачиваются.
Поляризация света
Поляризация света - это явление выделения из пучка естественного света лучей с определенной ориентацией электрического вектора.
Как же получить поляризованный свет?
Французским инженером Э. Малюсом в году был открыт названный в его честь закон. В экспериментах Малюса свет последовательно пропускался сквозь пару одинаковых пластинок из турмалина (прозрачное кристаллическое вещество зеленоватого оттенка). Они могли поворачиваться друг относительно друга на угол , как это проиллюстрировано на рисунке
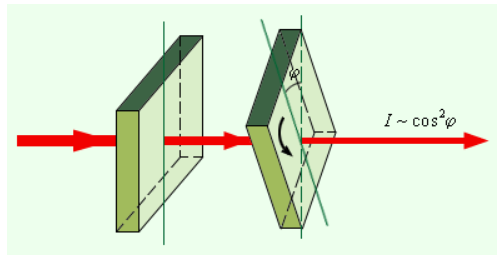
Рисунок Наглядный пример закона Малюса.
Интенсивность прошедшего света оказалась прямо пропорциональной :
.
Двойное лучепреломление точно также, как и закон Малюса не может быть объяснено с точки зрения теории продольных волн. Для продольных волн направление распространения луча представляет собой ось симметрии. В них любые направления в плоскости, нормальной, то есть перпендикулярной, лучу, равноправны.
В поперечной волне, к примеру, в бегущей по резиновому жгуту волне, направление колебаний и перпендикулярное ему направление не равноправны (рис. ).
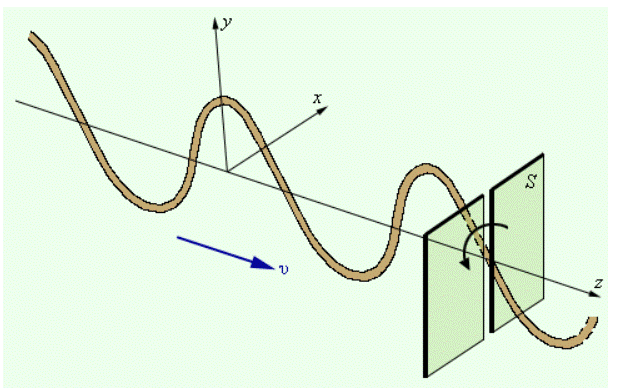
Рисунок Поперечная волна в резиновом жгуте. Частицы совершают колебательные движения вдоль оси . При повороте щели затухнет волна.
Выходит, что асимметрия относительно направления распространения луча – это решающий признак, отличающий поперечную и продольную волны. Первым высказал догадку о поперечности световых волн Т. Юнг в году. Независимо от Юнга Френель тоже выдвинул концепцию поперечности световых волн, и даже смог обосновать ее с помощью большого количества опытов. Им была создана теория двойного лучепреломления света в кристаллах.
В середине -х годов XIX века Максвелл, взяв за основу совпадение известных значений скоростей распространения света и электромагнитных волн, сделал вывод о природе света. Ученый решил, что свет – это частный случай электромагнитных волн. К тому времени экспериментальным путем была подтверждена поперечность световых волн. По этой причине Максвелл предположил, что она является еще одним важным аргументом в пользу его выводов насчет электромагнитной природы света.
Пропала необходимость во введении особой среды распространения волн – эфира, который приходилось рассматривать как твердое тело. Благодаря этому электромагнитная теория света приобрела должную стройность.
В условиях электромагнитной волны вектора и направлены перпендикулярно друг к другу и находятся в плоскости, которая перпендикулярна направлению распространения волны плоскости. (рис. )
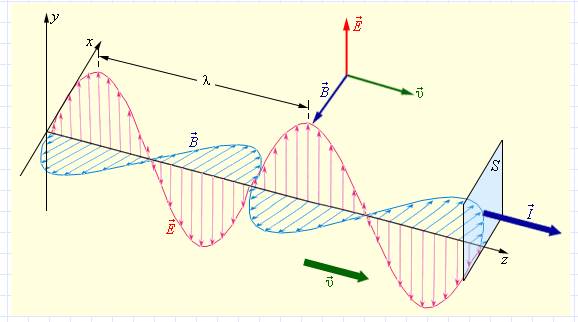
Рисунок Синусоидальная (гармоническая) электромагнитная волна. Векторы , и взаимно перпендикулярны.
В каждом из процессов взаимодействия света с веществом электрический вектор играет основную роль. По данной причине его называют световым вектором.
Виды поляризации света
Если при распространении электромагнитной волны световой вектор сохраняет свою ориентацию, то подобная волна носит название линейно поляризованной или плоско поляризованной. Отметим, что термин поляризации волн ввел Малюс применительно к поперечным механическим волнам.
Плоскость, в которой колеблется световой вектор , носит название плоскости колебаний (то есть плоскость , изображенная на рисунке ), а плоскость, в которой совершает колебание магнитный вектор , является плоскостью поляризации (плоскость на рисунке ).
В случае, когда две поляризованные в двух взаимно перпендикулярных плоскостях монохроматические волны распространяются вдоль одного и того же направления, в общем случае результатом их сложения будет эллиптически поляризованная волна (смотрите рисунок ).
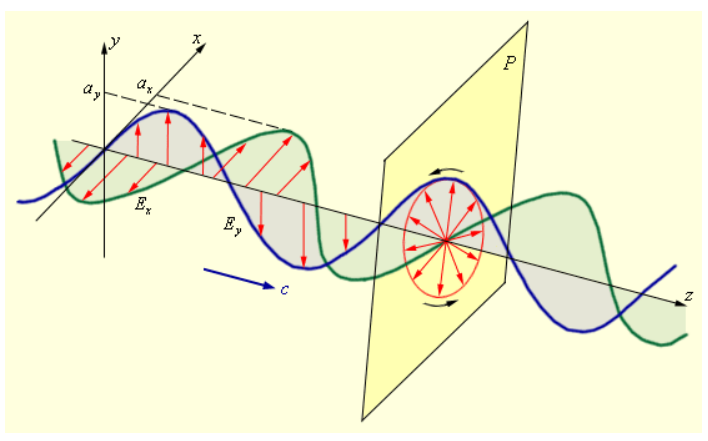
Рисунок Сложение двух взаимно перпендикулярно поляризованных волн и образование эллиптически поляризованной волны.
В нормальной (то есть перпендикулярной) направлению распространения волны эллиптически поляризованной волне в каждой плоскости конец результирующего вектора за период светового колебания обходит некоторый эллипс, носящий название эллипса поляризации.
Его размер и форма характеризуются амплитудами и линейно поляризованных волн и фазовым сдвигом между ними.
Волна, обладающая круговой поляризацией представляет собой частный случай эллиптически поляризованной волны.
Данные, получаемые при просмотре рисунка , дают представление о пространственной структуре эллиптически поляризованной волны.
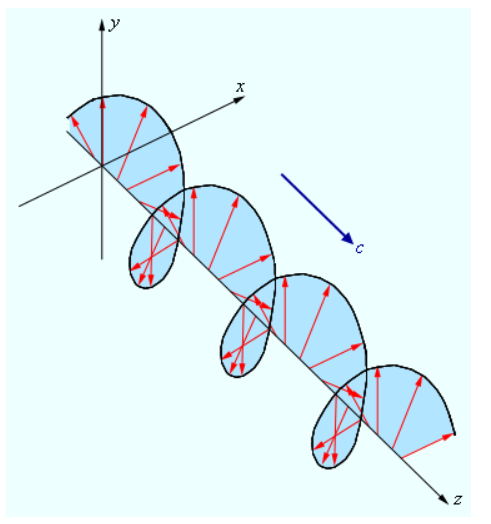
Рисунок Электрическое поле в эллиптически поляризованной волне.
Линейно поляризованный свет производится лазерными источниками. В случае отражения или рассеяния свет может стать поляризованным. В частности, голубой свет от неба частично или полностью поляризован. Однако, свет, который испускают обычные источники, такие как, например, солнечный свет и излучение ламп накаливания, является неполяризованным. Свет, исходящий от подобных источников, в любой момент состоит из вкладов огромного числа независимо излучающих атомов, обладающими различной ориентацией светового вектора в волнах, которые они излучают. По этой причине в результирующей волне вектор хаотично меняет свою ориентацию во времени, из-за чего в среднем все направления колебаний получаются равноправными.
Неполяризованный свет также называют естественным светом.
В любой момент времени вектор может быть спроецирован на две взаимно перпендикулярные оси (смотри рисунок ).
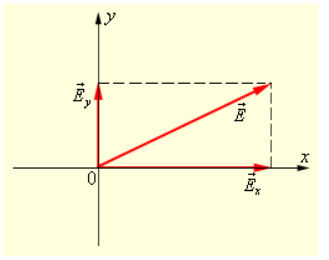
Рисунок Разложение вектора по осям и .
Это значит, что любую волну, вне зависимости от того, поляризованная она или же нет, можно представить в виде суперпозиции двух линейно поляризованных во взаимно перпендикулярных направлениях волн: . В поляризованной волне обе составляющие и когерентны, то есть разность фаз между и не претерпевает изменений, а в неполяризованной – некогерентны, значит разность фаз представляет собой случайную функцию времени.
Явление двойного лучепреломления света основывается на том, что в кристаллических веществах показатели преломления линейно поляризованных во взаимно нормальных направлениях волн, зачастую различны. По данной причине кристалл раздваивает лучи, которые проходят сквозь него так, как это показано на рисунке Два луча на выходе кристалла линейно поляризованы во взаимно перпендикулярных направлениях.
Кристаллы, в которых происходит двойное лучепреломление, называются анизотропными.
Прибегая к разложению вектора на составляющие по осям, можно объяснить закон Малюса (рис. ).
У значительной части кристаллов поглощение света кардинально зависимо от направления электрического вектора в световой волне. Такое явление носит название дихроизма.
В частности, данным свойством обладают использованные в знакомых нам опытах Малюса пластины турмалина. При некоторой толщине пластинка турмалина практически полностью поглощает одну из взаимно перпендикулярно поляризованных волн (как, к примеру, ) и частично пропускает вторую волну (то есть ).
Направление колебаний электрического вектора в прошедшей волне является разрешенным направлением пластины.
Пластинка турмалина может применяться как для создания поляризационного света, то есть в качестве поляризатора, так и для анализа характера поляризации света, как анализатор.
В наше время часто применяются искусственные дихроичные пленки, называющиеся поляроидами.
Поляроиды пропускают практически всю волну разрешенной поляризации и не пропускают поляризованную в нормальном направлении волну. Исходя из всего вышесказанного, можно заявить, что поляроиды – это идеальные поляризационные фильтры.
Разберем последовательное прохождение естественного света через пару идеальных поляроидов и (рисунок ), чьи разрешенные направления развернуты друг относительно друга на угол . Первый поляроид в приведенном тандеме занимает место поляризатора. Он преобразовывает естественный свет в линейно поляризованный. Второй поляроид применяется в качестве анализатора.
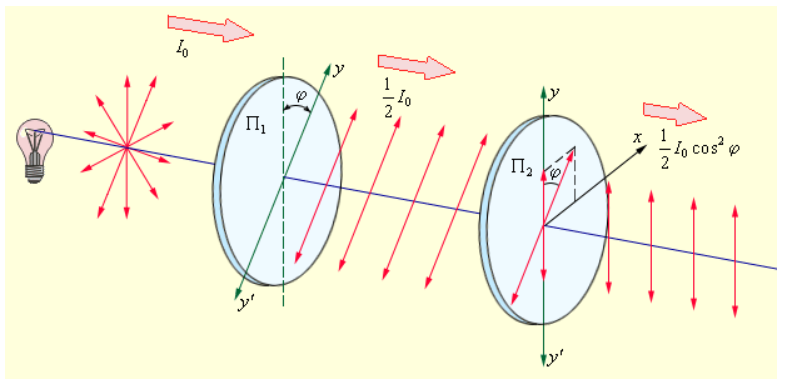
Рисунок Прохождение естественного света через два идеальных поляроида. представляет собой разрешенные направления поляроидов.
Обозначение амплитуды линейно поляризованной волны после прохождения света через первый поляроид в виде приводит к тому, что пропущенная вторым поляроидом волна приобретает амплитуду . Таким образом, интенсивность линейно поляризованной волны на выходе второго поляроида может быть записана в виде следующего выражения:
.
Выходит, что в электромагнитной теории света закон Малюса находит естественное объяснение, чья основа заключается в разложении вектора на его составляющие.
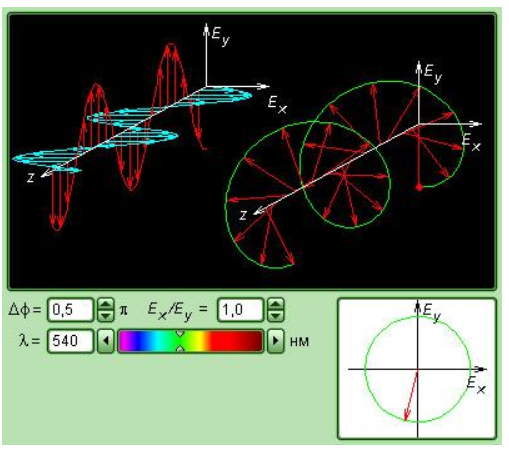
Рисунок Модель поляризации света.
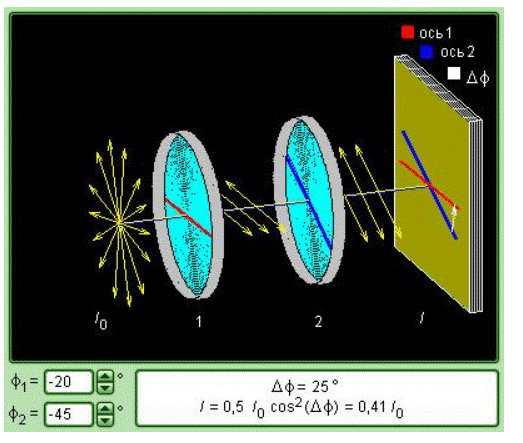
Рисунок Модель закона Малюса.
Навигация по статьям
