
Статью подготовили специалисты образовательного сервиса Zaochnik.
Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля
Содержание:
Дифракция света – это явление отклонения света от прямолинейного направления его распространения во время прохождения рядом с препятствиями.
Из опыта видно, что определенные условия влияют на захождение геометрической тени на область.
Когда на пути встречается препятствие в виде диска, шарика или круглого отверстия, тогда экран, расположенный на большом расстоянии, покажет дифракционную картину, то есть систему чередующихся светлых и темных колец. При отверстии линейного характера (щели или нити) экран показывает параллельные дифракционные полосы.
Принцип Гюйгенса-Френеля
Существование дифракционных явлений было задолго до времен Ньютона. Объяснение, основанное на корпускулярной теории, не давало должных результатов. Одним из первых объяснений явления дифракции, основанное на волновых представлениях, было дано Т. Юнгом. Еще в году была известна и развита количественная теория дифракционных явлений О. Френеля. Принцип Гюйгенса был заложен в основу. Он только дополнил при помощи идеи об интерференции вторичных волн.
Первоначальный вид данного принципа давал возможность нахождения положения фронтов в последующие моменты времени, иначе говоря, определял направление распространения волны. Это и есть принцип геометрической оптики. Впоследствии гипотеза Гюйгенса об огибающих вторичных волнах были заменены Френелем с помощью физически ясного положения, тогда вторичные волны в точке наблюдения интерферировали друг с другом.
Принципом Гюйгенса-Френеля считалась гипотеза, которая была со временем подтверждена. При решении задач, где необходимо использовать данный принцип, получение результата достаточно точное. На иллюстрации изображен принцип Гюйгенса-Френеля.
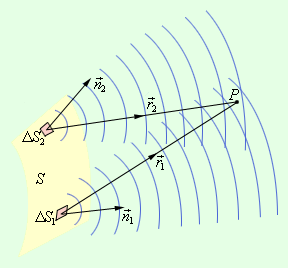
Рисунок Принцип Гюйгенса-Френеля. и – элементы волнового фронта, и - заданные нормали.
Предположим, что поверхность – положение волнового фронта в некоторый момент. Из теории волн известно, что он является поверхностью, где в заданных точках происходит колебание с одинаковым значением фазы. Волновыми фронтами плоской волны считают семейством параллельных плоскостей, которые перпендикулярно направлены относительно распространения волны. Волновые фронты сферической волны, которые испускаются при помощи точечного источника, относят к концентрическим сферам.
Для определения колебания в заданной точке , которое вызвано волной, используя принцип Френеля, находят колебания, которые вызваны в этой точке с помощью отдельных вторичных волн, которые приходят от элементов поверхности (, и так далее). Далее следует произвести сложение колебаний, учитывая амплитуды и фазы. Элементы, загороженные препятствиями, не учитываются при решении.
Для примера ниже приведена дифракционная задача прохождения плоской монохроматической волны, которая исходит от удаленного источника через отверстие с радиусом непрозрачного экрана.
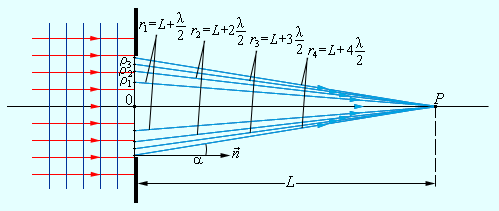
Рисунок Дифракция плоской волны на экране, содержащем круглое отверстие.
– точка наблюдения, находящаяся на оси симметрии, располагаемого на расстоянии относительно экрана. По принципу Гюйгенса-Френеля распределить на волновой поверхности вторичные источники, совпадающие с плоскостью отверстия, где волны достигают точки . Интерференция волн в этой точке является причиной возникновения результирующего колебания, квадрат амплитуды которого определяется при наличии значений длин волн , амплитуды падающей волны и расположением элементов.
Чтобы расчеты были облегченными, волновая поверхность падающей волны разбивается на кольцевые зоны, называемыми зонами Френеля, исходя из правила: расстояния от границ соседних зон к точке имеют отличие на половину волны.
Иначе говоря,
При рассмотрении волновой поверхности исходя из точки , тогда получим, что границы зон Френеля будут иметь вид концентрических окружностей. Наглядно это изображено на рисунке.
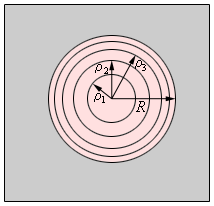
Рисунок Границы зон Френеля в плоскости отверстия.
По рисунку определяем радиусы зон по формуле: .
Зоны Френеля. Интерференционный максимум
Из определений раздела оптики имеем, что , тогда при решении можно пренебречь вторым подкоренным выражением. Для определения количества зон Френеля, которые укладываются на отверстии, используется формула, включающая в себя значение радиуса : .
Значение m может быть любым числом. От него зависит результат интерференции вторичных волн, проходящих точку . Такие открытые зоны Френеля обладают одинаковым значением площади:
.
По теории равные площади возбуждают колебания с одинаковой амплитудой в точке наблюдения. Но каждая последующая зона угла , располагаемая между лучом, проводимым к точке наблюдения, и нормалью относительно волновой поверхности, возрастает. Предположения Френеля говорит о том, что при увеличении угла происходит незначительное уменьшение колебаний, то есть:
, где обозначает амплитуду колебаний, которые были вызваны при помощи -ой зоны.
Используя приближение, видно, что амплитуда колебаний, которая вызвана определенной зоной, равняется среднему арифметическому соседних зон. Иначе это запишем как .
Отличие от двух соседних точек расстоянием говорит о том, что колебания, возбуждаемые этими зонами в состоянии противофазы. Соседние волны начинают гасить друг друга, а это приводит к тому, что суммарная амплитуда в точке запишется как:
.
Отсюда делаем вывод, что суммарная амплитуда в точке меньше колебаний, вызванных только при помощи одной зоны Френеля. Если все имеющиеся зоны Френеля являлись открытыми, тогда к точке наблюдения двигалась волна с амплитудой , невозмущенная препятствием. Тогда запись принимает вид:
.
Выражения в скобках равняются нулю, значит, амплитуда, вызванная волновым фронтом, равняется половине действий первой зоны.
Когда отверстие непрозрачного экрана дает возможность только одной зоне Френеля быть открытой, тогда наблюдается возрастание амплитуды колебаний в количестве раз, а интенсивности – раз. При открытии двух зон действие становится равным нулю. При наличии непрозрачного экрана с несколькими нечетными открытыми зонами, очевидно, что произойдет резкое возрастание амплитуды. При открытии зон получим, что .
Полученные пластинки обладают свойством фокусировки света, поэтому их называют зонными пластинками.
Круглый диск дает понять, что при дифракции зоны Френеля от до будут в закрытом состоянии. Отсюда получаем, что формула амплитуды колебаний примет вид:
Иначе можно записать как , ибо выражения в скобках будут равняться нулю.
Когда диск может закрыть небольшие зоны, тогда и , можно наблюдать интерференционный максимум. Иначе его называют пятном Пуассона, которое окружается дифракционными кольцами светлого и темного цвета.
Чтобы углубиться в понятие, необходимо оценить зоны Френеля. Имеется дифракционная картина на экране с расстоянием равным , а значение длины волны света (красный). Отсюда получим, что радиусом первой зоны является .
Так как оптический диапазон имеет короткую волну, тогда соответственно зона Френеля также мала. Отчетливее проявление дифракционных явлений заметно при небольшом количестве зон на препятствии.
Получим формулы вида:
или .
Название данного соотношения - критерий наблюдения дифракции.
Когда количество зон Френеля из препятствия увеличивается, тогда дифракционные явления становятся незаметными:
или .
Определение границы применимости геометрической оптики возможно при помощи заданного неравенства. При выполнении данного условия узкий пучок света может быть сформирован.
Отсюда следует вывод, что волновая оптика – это предельный случай геометрической.
Выше рассмотренный случай относится к дифракции света с удаленным источником, располагаемом на препятствиях округлой формы. При расположении точечного источника света на конечном расстоянии сферически расходящаяся волна должна падать на препятствие. Данный случай усложняет задачу. Тогда построение зон Френеля необходимо выполнять на поверхности сферической формы, показанное на рисунке .
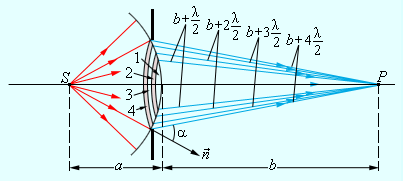
Рисунок Зоны Френеля на сферическом фронте волны.
При расчете видно, что радиусы зон Френеля на волне сферического фронта запишется, как
.
Выводы по теории Френеля справедливы.
Дифракция и интерференция света применима к любым волнам, так как имеется общность закономерностей. Начало XIX века – это было время, когда ученые только начинали изучать волны, а физическая природа света еще не была раскрыта.
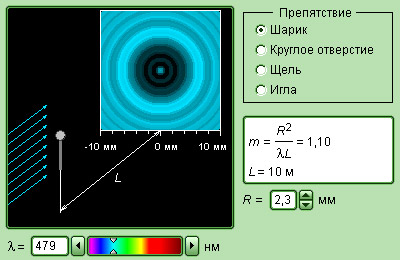
Рисунок Модель дифракции света.
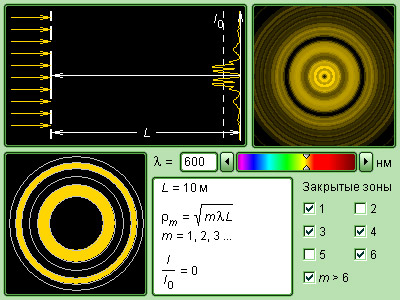
Рисунок Модель зоны Френеля.
Навигация по статьям
