
Статью подготовили специалисты образовательного сервиса Zaochnik.
Амплитудные и фазовые дифракционные решетки
Содержание:
Начнем с того, что узнаем, что такое дифракционная решетка.
Дифракционной решеткой – это прибор, благодаря которому осуществляется периодическая модуляция падающей волны света по фазе и амплитуде.
Амплитудная дифракционная решетка
Допустим, что у нас есть одномерная амплитудная решетка, в которой находятся затемненные промежутки и параллельные щели. Число щелей равно , ширину щелей обозначим как , а период решетки как .
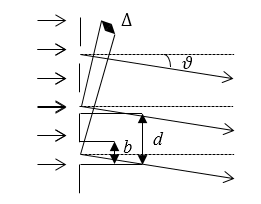
Рисунок
Если свет падает на нее нормально, то мы можем определить разность хода (дельту) монохромного света, испускаемого соседними щелями:
Фазовый сдвиг рассчитывается по формуле:
Здесь обозначает пространственную частоту. Результирующая амплитуда будет равна сумме геометрической прогрессии:
Амплитуда поля после прохождения одной щели здесь обозначена как .
Чтобы найти интенсивность света, который проходит сквозь амплитудную дифракционную решетку, нужно воспользоваться формулой:
Параметр – интенсивность света, падающего на решетку, – интенсивность той части света, который проходит через одну щель, а – интенсивность с учетом многолучевой интерференции.
Интенсивность всех пучков света в этом случае будет одинаковой.
Функция будет иметь нулевой числитель и знаменатель, если будет выполняться условие главных максимумов.
Таким образом, если данные максимумы будут выполнены, то свет, совершающий дифракцию на решетке с -ным количеством щелей, увеличит свою интенсивность в раз. Данная зависимость обусловлена таким явлением, как многолучевая интерференция пучков, проходящих через регулярные структуры.
Из формулы, приведенной выше, можно сделать вывод, что чем выше порядок, тем меньше интенсивность главных максимумов. Также имеется зависимость от отношения – целое число.
Если максимумы порядков , и т.д. будут приходиться на минимумы дифракции в одних щелях, то интенсивность света снизится до нуля. Например, при мы будем наблюдать равенство прозрачной и непрозрачной частей, в спектре решетки при этом останутся только главные максимумы нечетных и нулевых порядков, а четных среди них не останется совсем.
Если число щелей в решетке равно , то она будет создавать в промежутках между максимумами минимальную освещенность и побочных максимумов. Чем больше будет щелей, тем меньше будет относительная интенсивность дополнительных максимумов. При достижении определенного предела их существованием и вовсе можно пренебречь.
Если же свет падает на решетку наклонно, то пространственная частота будет отличаться от нуля, и условие главных максимумов станет частью разности пространственных частот. Образование пространственного спектра дифракционной решетки будет подчиняться принципам Фурье.
Дифракционная решетка имеет следующие характеристики спектральных свойств:
- угловую дисперсию : ;
- разрешающую способность : ;
- свободную дисперсионную область : (данная величина определяет диапазон спектра, свободный от перекрытия).
Сочетание свойств амплитудных дифракционных решеток делает их невыгодными для использования на практике. Они разбрасывают свет по многим порядкам, а основная часть энергии в них приходится на ахроматический нулевой порядок, и в максимумы высоких порядков в итоге попадает недостаточно света.
Фазовая дифракционная решетка
Такой тип решеток имеет гораздо лучшие спектральные свойства. Они характеризуются определенным профилем штрихов.
Фазовые дифракционные решетки бывают прозрачными и отражательными. Оба типа практически не оказывают влияния на амплитуду волны света, однако периодически влияют на ее фазу.
Если у нас есть отражательная решетка с профилированным штрихом, то максимум эффективности света, прошедшего дифракцию, будет наблюдаться в направлении отражения от плоскости штриха. Если же ширина рабочей грани занимает период решетки , то при она создаст всего один главный максимум порядка . Угол при этом условии называется углом блеска. Чтобы направить максимум энергии в первый порядок прозрачной фазовой решетки, нужно, чтобы для угла отклонения выполнялись сразу два условия.
Условие: сформулируйте объяснение, чем именно определяется разрешающая способность дифракционной решетки.
Решение
Мы можем определить разрешающую способность данного типа решеток следующим образом:
.
Если у решетки много штрихов (под "много" здесь подразумевается несколько десятков тысяч), то она имеет высокую разрешающую способность. Чтобы увеличить значение данного показателя, нужно увеличить порядки интерференции , однако их количество ограничено углами отклонения . Значит, в выражении не может превышать единицы.
Следовательно, . В итоге получаем, что:
.
Таким образом, чем больше , тем лучшую угловую дисперсию будет иметь решетка.
.
Из приведенной выше формулы мы можем вывести, что:
.
Значит, .
Данное выражение означает, что чем меньше , тем выше угловая дисперсия. На практике большее значение будут иметь решетки значительной общей ширины и с большим .
Условие: охарактеризуйте отличия фазовой дифракционной решетки с точки зрения картины интерференции.
Решение
Интерференционная картина для нее имеет неизменный характер. Меняться будет только распределение интенсивностей. Максимум при этом будет размещаться не в главном максимуме на угле , а на том максимуме, что попадет на угол или же будет размещаться рядом с ним. Это позволит нам работать с высокими порядками интерференции, поскольку разрешающая способность решетки будет выше (без уменьшения потерь интенсивности).
Навигация по статьям
