
Статью подготовили специалисты образовательного сервиса Zaochnik.
Дифракционный предел разрешения оптических инструментов
Содержание:
Случай дифракции света с препятствием, имеющим открытую малую часть -й зоны Френеля, представляет особый интерес для практики. Дифракционная картина в данном случае или , наблюдается при больших расстояниях. Когда , , тогда расстояние будет более двух метров. Такие проведенные в далекую точку лучи считаются параллельными. Данный случай рассматривается как дифракция в параллельных лучах или дифракция Фраунгофера.
Дифракция Фраунгофера. Формулы
Главное условие дифракции Фраунгофера – это наличие зон Френеля, проходящих через точку волны, являющихся плоскими относительно друг друга.
При расположении собирающей линзы за препятствием прохождения лучей под углом они сходятся в некоторой точке плоскости. Это показано на рисунке Отсюда следует, что любая точка в фокальной плоскости линзы эквивалентна бесконечно удаленной точке в отсутствии линзы.
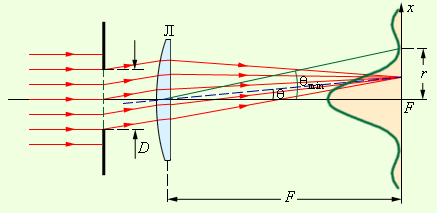
Рисунок Дифракция в параллельных лучах. Зеленая кривая – распределение интенсивности в фокальной плоскости (масштаб увеличен по оси ).
Теперь доступна дифракционная картина Фраунгофера, располагаемая в фокальной плоскости линзы. Исходя из геометрической оптики, фокус должен иметь линзу с точечным изображением удаленного предмета. Изображение такого предмета размывается по причине наличия дифракции. Это и есть проявление волновой природы света.
Оптическая иллюзия не дает точечного изображения. Если дифракция Фраунгофера с круглым отверстием диаметра имеет дифракционное изображение, состоящее из диска Эйри, то на него приходится около энергии света с окружающими его светлыми и темными кольцами. Это показано на рисунке Полученное пятно принимают за изображение точечного источника и рассматривают как дифракцию Фраунгофера на отверстии.
Для определения радиуса центрального пятна фокальной плоскости линзы используется формула .
Оправа линзы обладает свойством дифракции света, если лучи падают на нее, то есть выполняет роль экрана. Тогда обозначается как диаметр линзы.

Рисунок Дифракционное изображение точечного источника (дифракция на круглом отверстии). В центральное пятно попадает около энергии света.
Дифракционные изображения имеют очень маленькие размеры. Центральное светлое пятно в фокальной плоскости с диаметром линзы , фокусным расстоянием , длиной волны в монохроматическом свете имеет значение около . Сильное искажение маскируется в фотоаппаратах, проекторах по причине несовершенной оптики. Только высокоточные астрономические приборы могут реализовать дифракционный предел качества изображений.
Дифракционное размытие двух близко расположенных точек может дать результат наблюдения за одной точкой. Когда астрономический телескоп настроен на наблюдение за двумя близкими звездами с угловым расстоянием , то дефекты и аберрации устраняются, за счет этого фокальная плоскость объектива выдает дифракционные изображения звезд. Это рассматривается в качестве дифракционного предела объектива.
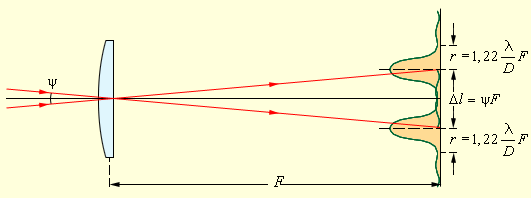
Рисунок Дифракционные изображения двух близких звезд в фокальной плоскости объектива телескопа.
Вышеуказанный рисунок объясняет, что расстояние между центрами дифракционных изображений звезд превышает значение радиуса центрального светлого пятна. Данный случай позволяет воспринимать изображение раздельно, значит, есть возможность видеть одновременно две близко расположенные звезды.
Если уменьшить угловое расстояние , тогда произойдет перекрывание, что не позволит видеть сразу две близкие звезды. В конце XIX века Дж. Релей предложил считать разрешение условно полным при расстоянии между центрами изображений равно радиусу Диска Эйри. Рисунок подробно показывает данный процесс. Равенство считают критерием решения Релея. Отсюда следует, что или .
Если телескоп имеет диаметр объектива , тогда есть возможность разрешения двух звезд при нахождении на угловом расстоянии (для ). Так как разрешающая способность не может быть более значения , то ограничение производится с помощью дифракционного предела космического телескопа, а по причине атмосферных искажений.
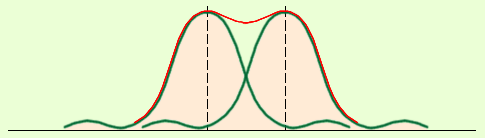
Рисунок Предел решения по Релею. Красная кривая – распределение суммарной интенсивности света.
Начиная с года, космический телескоп Хаббла был выведен на орбиту с зеркалом, имеющим диаметр . Предельным угловым разрешением телескопа на длине волны считают значение . Работа космического телескопа не зависит от атмосферных возмущений. Следует ввести величину , которая обратная величине предельного угла .
Иначе говоря, величина называется силой телескопа и записывается как .
Чтобы увеличить разрешающую способность телескопа, увеличивают размер объектива. Эти свойства применимы для глаз. Его работа аналогична телескопу. Диаметр зрачка выступает в роли . Отсюда предположим, что , тогда для предельного углового разрешения глаза принимаем формулу .
Результат оценивается с помощью разрешающей способности глаза, которая выполняется, учитывая размер светочувствительных элементов сетчатки. Делаем вывод: световой пучок с диаметром и длиной волны , благодаря волновой природе света, испытывает дифракционное уширение. Угловая полуширина пучка относится к порядку , тогда запись полной ширины пучка на расстоянии примет вид .
На рисунке отчетливо видно, что при удалении от препятствия происходит трансформация пучка света.
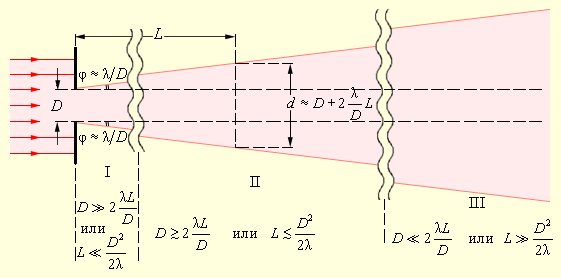
Рисунок Пучок света, расширяющийся вследствие дифракции. Область I – понятие луча света, законы геометрической оптики. Область II – зоны Френеля, пятно Пуассона. Область III – дифракция в параллельных лучах.
Изображение показывает угловое расхождение пучка и его уменьшение при увеличении поперечного размера . Данное суждение относится к волнам любой физической природы. Отсюда следует, что для посыла узкого пучка на Луну предварительно нужно произвести его расширение, то есть применить телескоп. При направлении лазерного пучка в окуляр он проходит все расстояние внутри телескопа с диаметром .
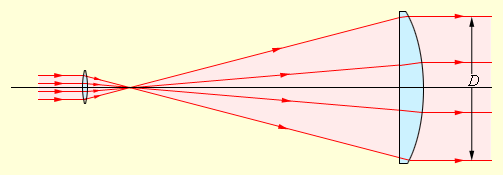
Рисунок Разрешение лазерного пучка с помощью телескопической системы.
Только при таких условиях пучок дойдет до поверхности Луны, а радиус пятна запишется как
, где обозначается как расстояние до Луны. Принимаем значение , , , получим . При направлении пучка с диаметром в его «засвет» на Луне был бы в виде пятна с радиусом в раз больше.
Разрешающая способность микроскопа
Микроскоп служит для наблюдения близко расположенных объектов, поэтому разрешающая способность зависит от линейного расстояния между близкими точками. Расположение объекта должно быть вблизи переднего фокуса объектива. Существует специальная жидкость, которой заполняют пространство перед объективом, что наглядно показано на рисунке Геометрически сопряженный объект, находящийся в этой же плоскости с его увеличенным изображением, рассматривается при помощи окуляра. Каждая точка размыта по причине дифракции света.
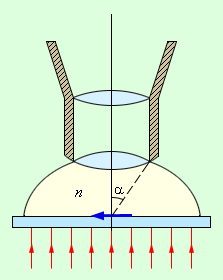
Рисунок Иммерсионная жидкость перед объективом микроскопа.
Предел разрешения объектива микроскопа был определен в г Г. Гельмгольцем. Такая формула записывается:
.
Знак требуется для обозначения длины волны, – для показателя преломления иммерсионной жидкости, – для обозначения апертурного угла. Величину называют числовой апертурой.
Качественные микроскопы имеют ампертурный угол , который приближен к значению предела . По формуле Гельмгольца наличие иммерсии позволяет улучшить предел разрешения. Предположим, что , , тогда .
Отсюда следует, что микроскоп не дает полной возможности просмотра каких-либо деталей с размерами намного менее размера длины световой волны. Волновые свойства света влияют на предел качества изображения объекта, который получаем с помощью любой оптической системы.
Навигация по статьям
