Классическое описание диамагнетизма. Ларморовская прецессия

Все диамагнетики являются слабомагнитными веществами: если магнитного поля нет, то они не магнитятся. Разберем, как выглядит механизм намагничивания. Это поможет нам понять те причины, по которым парамагнетики и диамагнетики имеют разные знаки намагничивания, а также узнать, почему магнитная восприимчивость зависит от атомного строения вещества. Допустим, что у нас есть одноатомный газ. В отсутствие магнитного поля его электроны в атомах перемещаются по кругу вокруг ядра. Обозначим радиус траектории как $r$, а угловую скорость как ${\omega }_0$. Тогда формула вычисления центростремительной силы $F_c$, действующей на электрон, будет выглядеть так:

Величина центростремительной силы заметно больше, чем у тех сил, что действуют на электрон со стороны внешнего поля. Зная это, мы можем принять радиус траектории перемещения электрона за константу, в связи с чем вводится понятие жесткого атома.

Теорема Лармора

Начнем сразу с формулировки теоремы. Она гласит:

Возьмем внешнее магнитное поле, в котором движение электронов будет меняться. Направим силу внешнего поля так, чтобы она прошла перпендикулярно орбите электрона. Тогда направление силы Лоренца $\overrightarrow{F}$ будет продольным по отношению к радиусу орбиты и либо однонаправленным с $\overrightarrow{F_c}$, либо направленным противоположно этому радиусу.

Модуль силы воздействия магнитного поля на частицу будет равен:

$F=q_e\omega rB$.

Здесь $q_e$ обозначает заряд электрона по модулю, а $\omega$ – угловую скорость электрона, причем $\omega \ne {\omega }_0$. С учетом этого мы можем записать уравнение, описывающее движения электронов в магнитном поле:

$m{\omega }^{2}r=F_c\pm q_e\omega rB=m{\omega }_0^{2}r\pm q_e\omega rB$.

От того, как направлены по отношению друг к другу векторы магнитной индукции и угловой скорости, будет зависеть выбор знака в уравнении (плюс или минус). Мы знаем, что:

${\omega }^2-{\omega }_0^2=\left(\omega -{\omega }_0\right)\left(\omega +{\omega }_0\right)\approx 2∆\omega \omega . \left|∆\omega \right|=\left|\omega -{\omega }_0\right|\ll \omega$.

Тогда из уравнения выводится следующая формула:

$∆\omega =\pm \frac{q_{e}B}{2m}={\omega }_L$.

Дополнительная угловая скорость, которую электрон получает в магнитном поле, называется ларморовой. Ее общепринятое обозначение – ${\omega }_L$. В случае направленности $\overrightarrow{B}$ против данной угловой скорости мы получим:

$\overrightarrow{F}⇅\overrightarrow{F_c}$.

Значит, величина угловой скорости в данном случае будет снижаться, т.е. ${\omega }_L\uparrow \uparrow \overrightarrow{B}$. Если же $\overrightarrow{B}$ будет направлена туда же, куда и угловая скорость, то:

${\omega }_L=-\frac{q_{e}B}{2m}$.

Важно учитывать, что в уравнении заряд электрона меньше $0$.

Что такое ларморовская прецессия

Выясним, как будет двигаться атом, если индукция поля и угловая скорость поля взяты произвольно. Для этого нам потребуются обобщенные результаты для данных произвольно взятых величин. Отличительным свойством магнетиков является их способность порождать ориентированный круговой ток при внесении во внешнее магнитное поле, что обусловлено изменением движения электронов.

Движение электрона внутри атома по орбите можно сравнить с вращением волчка. Для него характерны все те свойства, которые наблюдаются у гироскопов, находящихся под воздействием внешних сил, в том числе прецессия.

Прецессия электронной орбиты возникает тогда, когда атом расположен во внешнем магнитном поле $\overrightarrow{B}$. Вращательный момент, действующий на орбиту электрона, будет равен:

$\overrightarrow{N}=\left[\overrightarrow{p_m}\overrightarrow{B}\right]$.

Вращательный момент стремится к установлению направления $\overrightarrow{p_m}$, которое соответствует направлению поля (а механический момент $\overrightarrow{M}$ при этом приобретает противоположное направление). Тогда под действием вращательного момента векторы $\overrightarrow{p_m}$ и $\overrightarrow{M}$ будут совершать прецессию вокруг направления $\overrightarrow{B}$.

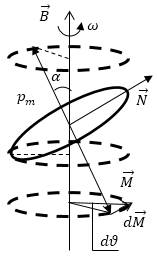
Рисунок $1$

Обозначим время вращения как $dt$. В течение него вектор механического момента увеличивается на $d\overrightarrow{M}$. Найти данное приращение можно по формуле:

$d\overrightarrow{M}=\overrightarrow{N}dt$.

Направление двух векторов $d\overrightarrow{M}$ и $\overrightarrow{N}$ будет перпендикулярным по отношению к той плоскости, в которой располагаются векторы $\overrightarrow{B}$ и $\overrightarrow{M}$. Найти модуль величины приращения можно так:

$dM=p_{m}B\sin \alpha dt$.

Буквой $\alpha$ обозначен угол, образуемый векторами $\overrightarrow{p_m}$ и $\overrightarrow{B}$.

За время $dt$ плоскость, в которой расположен вектор $\overrightarrow{M}$, совершит поворот вокруг вектора индукции. Угол поворота $d\upsilon$ можно вычислить так:

$d\upsilon =\frac{\left|d\overrightarrow{M}\right|}{M\sin \alpha }=\frac{p_{m}B\sin \alpha dt}{M\sin \alpha }=\frac{p_{m}Bdt}{M}$.

Отношение $\frac{d\upsilon }{dt}={\omega }_L$ – это и есть угловая скорость прецессии. Используя формулу, выведенную выше, запишем:

${\omega }_L=\frac{p_{m}B}{M}$.

Показатель $\frac{p_m}{M}$ – это магнитомеханическое (гиромагнитное) отношение. Его величину можно вычислить так:

$\frac{p_m}{M}=-\frac{q_e}{2m}$.

Буквой $m$ обозначена масса электрона, а минус перед второй частью равенства указывает на противоположность направлений моментов $\left(\overrightarrow{p_m}⇅\overrightarrow{M}\right)$.

Подставим справа найденную ранее величину и получим:

${\omega }_L=-\frac{q_{e}B}{2m}$.

Показатель ${\omega }_L$ – это частота ларморовой прецессии, или ларморова частота. Она независима от угла наклона орбиты, ее радиуса или скорости, с которой движется электрон, т.е. она одинакова для всех. Под влиянием прецессии возникает дополнительное движение электрона вокруг направления поля, которое, в свою очередь, рождает индуцированный магнитный момент. Он равен:

.

Буквой $Z$ обозначен атомный номер элемента. Направление индуцированного магнитного момента противоположно полю.

Следует отметить, что ларморова прецессия характерна не для всех веществ.

Что такое диамагнетизм

Мы уже выяснили, что ларморова прецессия способствует образованию кругового тока в веществе путем изменения движения электронов в атомах. В этом случае ток создает левовинтовую систему с определенным направлением вектора индукции магнитного поля. Получается, что та индукция, которую создает круговой ток, будет направлена навстречу вектору индукции, образуемой внешним магнитным полем. Тогда направление магнитного момента атома, возникающего при прецессии, и вектора намагниченности будут направлены противоположно вектору индукции внешнего поля. Следовательно, суть диамагнетизма состоит именно в ларморовой прецессии, наличии магнитного момента и дополнительного поля.