
Статью подготовили специалисты образовательного сервиса Zaochnik.
Магнитная проницаемость и магнитная восприимчивость вещества
Содержание:
При проведении опыта с соленоидом, соединенным с баллистическим гальванометром, во время включения тока в нем можно определить значение магнитного потока , который будет пропорционален отбросу стрелки гальванометра. Если делать его дважды с одинаково установленным током в гальванометре, то в первом опыте соленоид будет без сердечника, а во втором его введут перед включением тока.
Проведение второго опыта дает понять, что наличие магнитного потока значительно больше, чем в первом. Если повторить процесс, но с задействованием сердечника разной толщины, то получаем максимальный поток при полном заполнении соленоида железом, то есть при плотно навитой обмотке на сердечнике. Имеем, что:
где является магнитным потоком в катушке с сердечником, - магнитным потоком без сердечника.
Увеличение магнитного потока при введении сердечника в соленоид обусловлено появлением магнитного потока, создаваемого совокупностью ориентированных амперовых молекулярных токов, и присоединение его к уже имеющемуся магнитному потоку от тока обмотки соленоида. Происходит ориентировка молекулярных токов под влиянием магнитного поля, их суммарный момент больше не равняется нулю, потому как происходит возникновение дополнительного магнитного поля.
Магнитная проницаемость. Измерения
Величина характеризует магнитные свойства среды и называется магнитной проницаемостью (относительной магнитной проницаемостью).
Она является безразмерной характеристикой вещества. Если происходит увеличение потока в раз, это говорит о том, что магнитная индукция в сердечнике во столько же раз больше, чем в вакууме при том же токе в соленоиде. Запись примет вид:
, где означает магнитную индукцию поля в вакууме.
Вместе с магнитной индукцией, являющейся основной силовой характеристикой поля, применяют вспомогательную векторную величину – напряженность магнитного поля , которая связана с при помощи соотношения:
.
Если формула применится в опыте с сердечником, тогда при его отсутствии:
.
Значение . Если сердечник имеется, то
.
Равенство выполняется, поэтому
.
Отсюда следует, что напряженность магнитного поля не зависит от характера однородного вещества, которым было заполнено пространство. Большинство веществ имеет магнитную проницаемость, равную . Исключениями считаются ферромагнетики.
Магнитная восприимчивость вещества
Обычно связь вектора намагниченности и вектора напряженности в каждой точке магнетика обозначается:
.
является магнитной восприимчивостью. Величина безразмерная. Если вещество неферромагтиное и обладает небольшим полем, то не зависит от напряженности, является скалярной величиной.
Анизотропные среды предполагают в качестве тензора, направления и не совпадают.
Связь между магнитной восприимчивостью и магнитной проницаемостью
Из определения вектора напряженности магнитного поля:
.
При подстановке выражения в получаем:
.
Напряженность приобретает вид:
.
При сравнении и :
.
Магнитная восприимчивость может принимать как положительные, так и отрицательные значения. Из имеем, что может быть больше или меньше .
Произвести вычисление намагниченности в центре кругового витка с радиусом и током при погружении в жидкий кислород. Значение магнитной восприимчивости жидкого кислорода .
Решение
Следует применить выражение, которое показывает связь напряженности магнитного поля и намагниченности, то есть:
.
Далее произведем поиск поля в центре витка с током, так как необходимо вычислить намагниченность в этой точке.
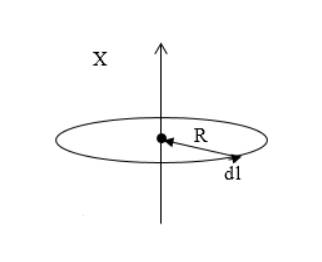
Рисунок
На проводнике с током необходимо выбрать элементарный участок, показанный на рисунке , как основу для решения задания. Применим формулу напряженности элемента витка с током.
Тогда:
.
Где – является радиус-вектором, проведенным из элемента тока в рассматриваемую точку,
– элемент проводника с током, – угол между и .
Опираясь на рисунок , , следует упрощение . Так как расстояние от центра окружности элемента проводника с током постоянно и равняется радиусу витка , получаем:
.
Направление результирующего вектора напряженности магнитного поля совпадает с осью . Его находят как сумму отдельных векторов , потому что все элементы тока создают в центре витка магнитные поля, которые направлены вдоль нормали витка. Используя принцип суперпозиции, полная напряженность магнитного поля находится при переходе к интегралу вида:
.
Произведем подстановку в :
.
Для нахождения намагниченности, следует подставить значение напряженности из в . тогда:
.
Вычисляем с числовыми выражениями:
.
Ответ: .
Произвести вычисление доли суммарного магнитного поля в вольфрамовом стержне, находящегося во внешнем однородном магнитном поле, которую определяют молекулярные токи. Значение магнитной проницаемости вольфрама равняется .
Решение
Нахождение индукции магнитного поля , приходящейся на долю молекулярных токов, представляется:
, где – является намагниченностью. Ее связь с напряженностью выражается через соотношение:
.
Магнитная восприимчивость находится из
.
Магнитное поле молекулярных токов будет равно:
.
По формуле находим полное поле в стержне:
.
Задействовав выражения , , найдем соотношение:
.
Подставим числовые выражения:
.
Ответ: .
Навигация по статьям
