
Статью подготовили специалисты образовательного сервиса Zaochnik.
Вихревой характер магнитного поля
Содержание:
Вихревой характер магнитного поля заключается в непрерывности линий индукции любого магнитного поля при отсутствии начала и конца, так как они либо замкнуты, либо уходят в бесконечность. На порождение полей не влияет характер контуров с током. Векторные поля, обладающие непрерывными силовыми линиями, называются вихревыми полями. Магнитное поле также можно считать вихревым.
Электростатические поля имеют силовые линии, начинающиеся и заканчивающиеся на электрических зарядах, причем, всегда находятся в разомкнутом состоянии. Линии магнитного поля замкнуты. Это говорит об отсутствии магнитных зарядов в природе.
Электрический ток образуется благодаря движению электрических зарядов. Так как магнитных зарядов нет, это объясняет отсутствие магнитного тока. Данное утверждение можно выразить при помощи уравнения:
Определение вихревого поля также выполнимо другим способом.
Вихревое магнитное поле
Векторные поля, вектор которых не равен нулю – это вихревые магнитные поля.
Следуя из теоремы о циркуляции локального вида, которая влияет на вихревой характер магнитного поля:
, где считается объемной плотностью тока, и второй формы определения вихревого поля можно заключить, что магнитное поле будет вихревым там, где проходят токи, а безвихревым там, где их нет.
При отсутствии токов вектор магнитной индукции представляется в виде градиента скалярного магнитного потенциала :
.
Если имеются токи, то данное представление невозможно.
Различие между потенциальными и вихревыми полями
Основными уравнениями магнитного поля постоянных токов считаются выражения вида:
.
Произведем сравнение с основными уравнениями электростатики:
.
Рассматривая систему , видно, что электрическое поле всегда потенциально, а его источниками являются электростатические (неподвижные) заряды.
Магнитное поле считается вихревым при наличии токов. Оно зависит от формы контура и не определяется только положением начала и конца этого контура. Существование однозначной разности потенциалов в магнитном поле исключено. Значение магнитного напряжения по замкнутому контуру не равняется нулю.
Электрические токи являются источниками поля. Магнитное поле считается вихревым, так как его дивергенция везде равна нулю. Его также называют соленоидальным. Определение потенциального электростатического поля возможно при заданной дивергенции напряженности в качестве функции координат. Полное определение вихревого магнитного поля реально, когда имеется мощность его вихрей, то есть как функция координат.
Показать, почему для вихревого магнитного поля нельзя представить вектор индукции в виде градиента магнитного потенциала .
Решение
Возьмем формулу:
.
Для выражения можно применить операцию :
.
Известно значение :
.
При подстановке в имеем:
.
Ответ: Вспомнив теорему о циркуляции, получаем отсутствие токов. В данном случае, представление вектора индукции магнитного поля невозможно в виде магнитного потенциала в области, где проходят токи.
Применение понятия скалярного магнитного потенциала возможно только в области пространства, где . Данная часть пространства характеризуется неоднозначностью функции. Показать это.
Решение
Необходимо рассмотреть магнитное поле возле контура с током, как изображено на рисунке . По теореме о циркуляции для любого контура выполнимо равенство:
.
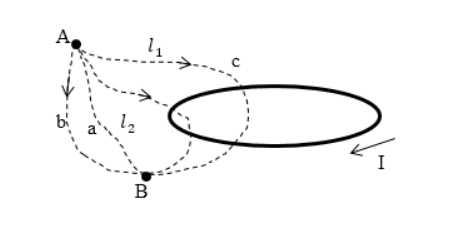
Рисунок
Если токов нет, магнитное поле становится потенциальным, интеграл, который необходимо взять между и , не зависит от пути интегрирования, то запись примет вид:
.
Отсюда следует:
.
Выражение может быть рассмотрено в качестве разности скалярных магнитных потенциалов в точках и . Можно пойти иным путем и принять значение потенциала равным нулю в точке , как выполнялось для нахождения потенциала в электростатике:
.
При выборе контура, охватывающего какой-либо ток (контур ), как показано на рисунке , линейный интеграл по замкнутому контуру от циркуляции вектора индукции по нему будет не равен нулю:
.
Или
Тогда:
.
При выборе какого-либо пути , охватывающего ток в количестве раз, имеем:
.
Следует задать нулевой потенциал в точке :
.
Ответ: Получив уравнение , очевидно, что скалярный магнитный потенциал является неоднозначной величиной.
Навигация по статьям
