
Статью подготовили специалисты образовательного сервиса Zaochnik.
Угловое ускорение
Содержание:
Система понятий кинематики включает в себя также такую величину как угловое ускорение тела. Дадим ей определение, рассмотрим основные аспекты с использованием примеров.
Основные понятия
Угловое ускорение – величина, характеризующая изменение скорости с течением времени.
Пусть рассматриваемый промежуток времени это: , а изменение угловой скорости составит , тогда числовое значение среднего углового ускорения за тот же интервал времени: . Перейдем к пределу, когда , тогда формула углового ускорения будет иметь вид: .
Числовое значение ускорения в заданный момент времени есть первая производная от угловой скорости или вторая производная от угла поворота по времени.
Размерность углового ускорения (т.е. ). Укажем также, в чем измеряется угловое ускорение: за единицу измерения стандартно принимается или иначе: .
Ускоренное вращение тела – это вращение, при котором угловая скорость (ее модуль) возрастает с течением времени.
Замедленное вращение тела – это вращение, при котором угловая скорость (ее модуль) убывает с течением времени.
В общем, довольно просто заметить, что, если и имеют одинаковые знаки, наблюдается ускоренное вращение, а, когда противоположные знаки – замедленное.
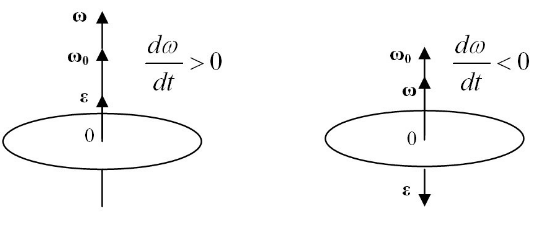
Рисунок . Вектор углового ускорения
Если мы представим угловое ускорение как вектор , имеющий направление вдоль оси вращения, то в случае ускоренного вращения
рисунка ) и будут противоположны по направлениям в случае замедленного вращения (правая часть
рисунка ).
Закон равнопеременного вращения
Равнопеременное вращение – вращение, при котором угловое ускорение во все время движения является постоянным .
Выведем формульно закон равнопеременного вращения. Пусть в начальный момент времени угол вращения равен ; угловая скорость - (т.е. является начальной угловой скоростью).
Выражение дает нам возможность сделать запись: . Проинтегрируем левую часть крайней записи в пределах от до , а правую – в пределах от до , тогда:
.
Проинтегрируем вторично и получим формулу, выражающую закон равнопеременного вращения:
Закон равнопеременного вращения: .
Вращение является равноускоренным, когда и имеют одинаковые знаки.
Вращение является равнозамедленным, когда и противоположны по знаку.
Угловое ускорение имеет связь с полным и тангенциальным ускорениями. Пусть некоторая точка вращается неравномерно по окружности с радиусом , тогда: . Нормальное ускорение имеет также связь с угловым: . Учтем это выражение и для полного ускорения получим: Для равнопеременного движения: и .
Практические примеры
На рисунке заданы различные типы вращения гироскопа (волчка). С учетом соответствующих подписей необходимо указать, какой рисунок верно демонстрирует направление углового ускорения.
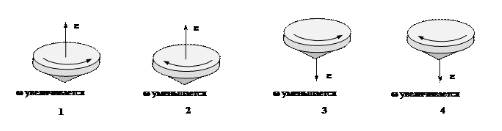
Рисунок
Решение
Правило буравчика (правого винта) связывает направление вращения и псевдовектор угловой скорости. Рисунки и показывают направление псевдовектора вверх, а рисунки и – вниз.
Когда угловая скорость возрастает, ее приращение и вектор ускорения совпадут с вектором угловой скорости (рисунки и ). Когда угловая скорость будет уменьшаться, ее приращение и вектор ускорения окажутся противоположно направлены вектору угловой скорости (рисунки и ). Таким образом, все рисунки демонстрируют верное направление углового ускорения.
Пусть задана некоторая материальная точка, совершающая движение по окружности с радиусом . При этом выражение отражает зависимость угла поворота от времени. Необходимо найти полное ускорение заданной точки как функцию времени.
Решение
Запишем выражения для угловой скорости и углового ускорения заданной точки:
.
Полное ускорение запишем как:
.
Навигация по статьям
