
Статью подготовили специалисты образовательного сервиса Zaochnik.
Криволинейное движение
Содержание:
В зависимости от формы траектории движение можно подразделять на прямолинейное и криволинейное. Чаще всего можно столкнуться с криволинейными движениями, когда траектория представлена в виде кривой. Примером такого вида движения является путь тела, брошенного под углом к горизонту, движение Земли вокруг Солнца, планет и так далее.
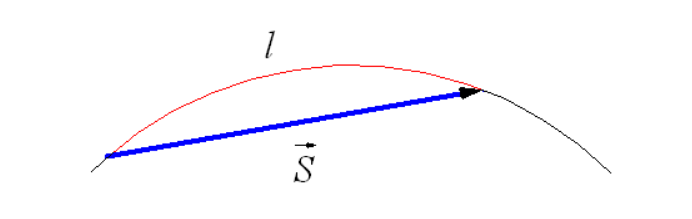
Рисунок . Траектория и перемещение при криволинейном движении
Мгновенная скорость при криволинейном движении
Криволинейным движением называют движение, траектория которого представляет собой кривую линию. Если тело движется по криволинейной траектории, то вектор перемещения направлен по хорде, как показано на рисунке , а является длиной траектории. Направление мгновенной скорости движения тела идет по касательной в той же точке траектории, где в данный момент располагается движущийся объект, как показано на рисунке .
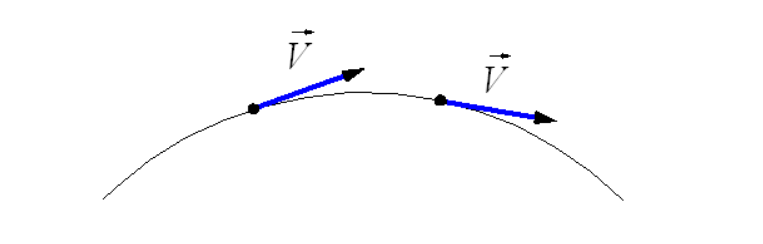
Рисунок . Мгновенная скорость при криволинейном движении
Криволинейное движение материальной точки называют равномерным тогда, когда модуль скорости постоянный (движение по окружности), и равноускоренным при изменяющемся направлении и модуле скорости (движение брошенного тела).
Криволинейное движение всегда ускоренное. Это объясняется тем, что даже при неизмененном модуле скорости, а измененном направлении, всегда присутствует ускорение.
Для того чтобы исследовать криволинейное движение материальной точки, применяют два метода.
Путь разбивается на отдельные участки, на каждом из которых его можно считать прямолинейным, как показано на рисунке .

Рисунок . Разбиение криволинейного движения на поступательные
Теперь для каждого участка можно применять закон прямолинейного движения. Такой принцип допускается.
Разбиение на движения по дугам
Самым удобным методом решения считается представление пути в качестве совокупности нескольких движений по дугам окружностей, как показано на рисунке . Количество разбиений будет намного меньше, чем в предыдущем методе, кроме того, движение по окружности уже является криволинейным.
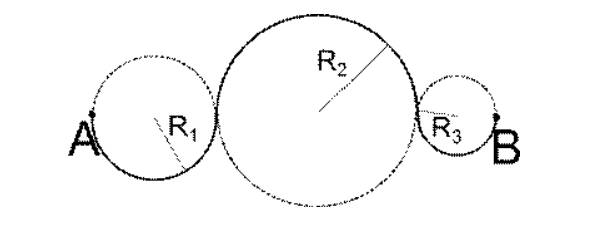
Рисунок . Разбиение криволинейного движения на движения по дугам окружностей
Для записи криволинейного движения необходимо уметь описывать движение по окружности, произвольное движение представлять в виде совокупностей движений по дугам этих окружностей.
Исследование криволинейного движения включает в себя составление кинематического уравнения, которое описывает это движение и позволяет по имеющимся начальным условиям определить все характеристики движения.
Дана материальная точка, движущаяся по кривой, как показано на рисунке . Центры окружностей располагаются на одной прямой. Необходимо найти перемещение
и длину пути во время движения из точки в .
Решение
По условию имеем, что центры окружности принадлежат одной прямой, отсюда:
.
Так как траектория движения – это сумма полуокружностей, то:
.
Ответ: , .
Дана зависимость пройденного телом пути от времени, представленная уравнением . Вычислить, через какой промежуток времени после начала движения ускорение тела будет равно
Решение
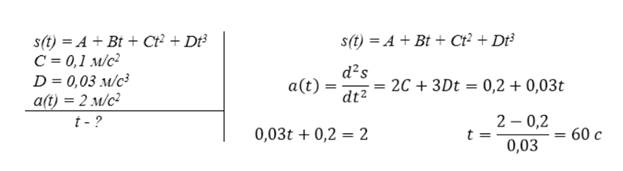
Ответ: .
Навигация по статьям
