
Статью подготовили специалисты образовательного сервиса Zaochnik.
Элементы гидро- и аэродинамики
Содержание:
Для того, чтобы описать такой сложный процесс, как движение жидкостей или газов, применяют разного рода упрощенные модели. Например, для упрощения используется предположение, что жидкость или даже газ несжимаемы и идеальны, не имеют внутреннее трение между слоями, которые движутся. Когда такая идеальная жидкость находится в движении, отсутствует переход механической энергии во внутреннюю, т.е. имеет место выполнение закона сохранения механической энергии. В свою очередь, из этого закона для стационарного потока идеальной и несжимаемой жидкости вытекает уравнение (принцип) Бернулли, которое было сформулировано в г.
Элементы гидродинамики. Уравнение Бернулли
Стационарный поток жидкости – это поток без образования вихрей. В этом случае частицы жидкости осуществляют перемещение по постоянным во времени траекториям, называемым линиями тока.
В рамках имеющегося опыта можно утверждать, что возникновение стационарных потоков возможно лишь тогда, когда скорость движения жидкости достаточно мала.
Возьмем для рассмотрения стационарное течение идеальной несжимаемой жидкости по трубе переменного сечения (рис. ). Различные части трубы располагаются на разных высотах.
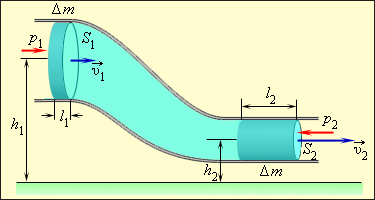
Рис. . Поток идеальной жидкости в трубе переменного сечения.
Рассматриваемая труба имеет два сечения: и ; - это время прохождения жидкости в трубе. Так, за через сечение жидкость осуществит перемещение на ; через сечение – на ( и – обозначение скоростей частиц жидкости в трубе соответствующих сечений). Условие несжимаемости будет иметь следующую запись: или , где является объемом жидкости, прошедшей через сечения и .
С переходом жидкости из участка трубы большего сечения в участок меньшего сечения скорость движения потока увеличивается: жидкость перемещается с ускорением. Это означает, что жидкость испытывает воздействие силы. Если речь идет о движении потока в горизонтальной трубе, можно утверждать, что возникновение этой силы возможно только как следствие разности давления в широком и узком участках трубы (в широком участке давление должно быть больше, чем в узком). В случае же, когда различные участки трубы располагаются на разной высоте, ускорение потока обусловлено совокупным воздействием силы тяжести и силы давления.
Сила давления есть упругая сила сжатия жидкости.
Явление несжимаемости жидкости означает только то, что возникновение упругих сил имеет место при пренебрежимо малом изменении объема любой части жидкости.
Поскольку действует предположение, что жидкость идеальна, ее протекание по трубе происходит без трения, а значит к ее движению уместно применять закон сохранения механической энергии.
В процессе движения жидкости силы давления выполняют работу, которую запишем так:
.
Работа сил давления есть изменение потенциальной энергии упругой деформации жидкости, взятое с обратным знаком.
Те изменения, которые происходят за промежуток времени в выделенной части жидкости, помещенной между участками трубы с сечениями и в начальный момент времени, в случае стационарного течения заключаются в перемещении массы жидкости из участка с сечением в участок сечением ( – плотность жидкости). На рисунке соответствующие объемы обозначены штриховкой. Закон сохранения механической энергии для этой массы будет иметь запись: . и здесь являются полными механическими энергиями массы в поле тяготения и записываются так:
.
Откуда можно вывести:
.
Выражение называется уравнением Бернулли.
Из уравнения Бернулли следует, что: на всей протяженности рассматриваемой трубы. В частном случае, когда труба расположена горизонтально, уравнение Бернулли принимает вид: .
Величина обозначает статическое давление в жидкости, которое возможно измерить, используя манометр, двигающийся вместе с жидкостью. В практике давление в различных сечениях трубы определяют при помощи манометрических трубок, размещаемых через боковые стенки в поток жидкости таким образом, чтобы нижние концы трубок были параллельны скоростям частиц жидкости (рис. ). Из уравнения Бернулли следует:
Давление в жидкости, проходящей по горизонтальной трубе переменного сечения, больше в тех сечениях потока, в которых скорость ее движения меньше, и наоборот, давление меньше в тех сечениях, в коих скорость больше.
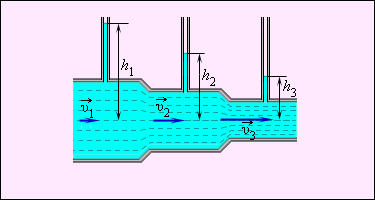
Рис. Использование манометров для определения давления в потоке.
В случае, когда сечение потока жидкости достаточно велико, уравнение Бернулли необходимо применять к линиям тока, т. е. линиям, вдоль которых происходит перемещение частиц жидкости при стационарном течении.
Мы имеем широкий сосуд с отверстием в боковой стенке, в котором течет идеальная несжимаемая жидкость. При движении потока из отверстия линии тока начинаются вблизи свободной поверхности жидкости и проходят через отверстие (рис. ).
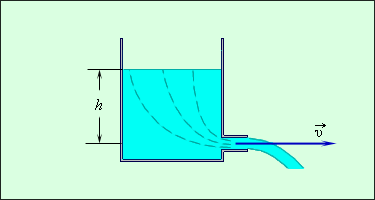
Рис. Истечение жидкости из широкого сосуда.
Так как скорость жидкости вблизи поверхности в широком сосуде является пренебрежимо малой, уравнение Бернулли примет вид: ,
где – атмосферное давление, – перепад высоты вдоль линии тока. Тогда: .
- это формула, выражающая скорость истечения потока и называемая формулой Торричелли. Скорость истечения идеальной жидкости из отверстия в сосуде такая же, как и при свободном падении тела с высоты без начальной скорости.
Элементы аэродинамики
Отличительной чертой газов от жидкостей является возможность значимо изменять свой объем. Расчеты позволяют утверждать, что сжимаемостью газов можно пренебречь, когда наибольшие скорости в потоке являются малыми по сравнению со скоростью звука в этом газе. Следовательно, уравнение Бернулли возможно использовать для достаточно широкого класса задач аэродинамики.
В числе подобных задач - исследование сил, осуществляющих воздействие на крыло самолета. Строго теоретически решить эту задачу достаточно затруднительно, и обычно для изучения сил используют экспериментальные методы. Уравнение Бернулли дает возможность только качественно объяснить появление подъемной силы крыла.
Рис. демонстрирует линии тока воздуха, обтекающего крыло самолета. Особый профиль крыла и наличие угла атаки (угла наклона крыла по отношению к набегающему потоку воздуха) определяют тот факт, что скорость течения воздуха над крылом становится больше, чем под крылом. В связи с этим на рис. линии тока над крылом расположены ближе друг к другу, чем под крылом. Выводом из принципа Бернулли является то, что давление в нижней части крыла будет больше, чем в верхней, и в итоге мы имеем силу
Подъемная сила дает возможность компенсации силы тяжести, осуществляющей действие на самолет, и этим она и определяет саму возможность движения тяжелых летательных аппаратов в воздушной среде.
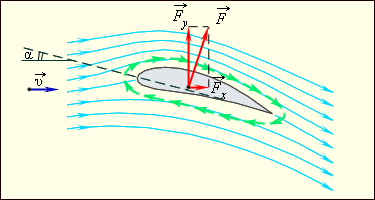
Рис. Линии тока при обтекании крыла самолета и возникновение подъемной силы. – угол атаки.
Теорию подъемной силы крыла самолета сформулировал Н. Е. Жуковский в г., и она получила название теоремы Жуковского:
Подъёмная сила сегмента крыла бесконечного размаха равна произведению плотности газа (жидкости), скорости газа (жидкости), циркуляции скорости потока и длины выделенного отрезка крыла. Направление действия подъёмной силы получается поворотом вектора скорости набегающего потока на прямой угол против циркуляции.
Жуковский продемонстрировал, что при обтекании крыла значимое влияние оказывают силы вязкого трения в поверхностном слое. Итогом их воздействия является возникновение кругового движения или циркуляции воздуха вокруг крыла (обозначено стрелками зеленого цвета на рис. ). В верхней части крыла скорость циркулирующего воздуха соединяется со скоростью набегающего потока, в нижней же части эти скорости противоположно направлены. Подобный эффект и служит причиной появления разности давлений и образования подъемной силы.
Циркуляция воздуха, определяемая силами вязкого трения, появляется и вокруг тела, которое вращается. Практически значимым, к примеру, является вращение цилиндра.
При вращении цилиндра само тело влечет за собой примыкающие слои воздуха, создавая циркуляцию воздушного потока. Когда цилиндр установлен в набегающем потоке, возникает сила бокового давления, подобная подъемной силе крыла самолета. Такое явление носит название эффекта Магнуса.
На рис. проиллюстрировано обтекание цилиндра, осуществляющего вращение, набегающим потоком. Примером эффекта Магнуса служит полет закрученного мяча при игре в теннис или футбол.
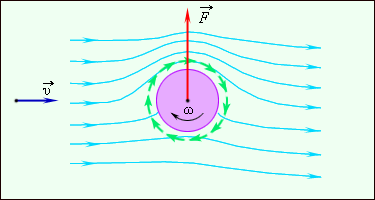
Рис. Обтекание вращающегося цилиндра набегающим потоком воздуха.
Таким образом, на множество явлений аэродинамики оказывают значимое влияние силы вязкого трения. Они дают толчок к возникновению циркулирующих потоков воздуха вокруг крыла самолета или вокруг вращающегося тела, к появлению силы сопротивления среды и т. д. Уравнение Бернулли не берет в расчет силы трения. Вывод Бернулли опирается на закон сохранения механической энергии при течении жидкости или газа. Поэтому при помощи принципа Бернулли невозможно исчерпывающе объяснить явления, в которых имеется проявление сил трения. В подобных случаях возможно опираться лишь на качественные соображения – чем больше скорость, тем меньше давление в потоке газа.
Особо заметное проявление имеют силы вязкого трения в потоке жидкостей. Некоторые жидкости обладают вязкостью такой значимой величины, что использование уравнения Бернулли может привести к качественно неверным результатам.
К примеру, в случае истечения жидкости высокой вязкости через отверстие в стенке сосуда ее скорость может быть в десятки раз меньше той, что будет рассчитана по формуле Торричелли. Когда сферическое тело движется в идеальной жидкости, оно не должно встречать лобового сопротивления. Когда такое тело перемещается в вязкой жидкости, появляется сила сопротивления, и ее модуль будет пропорционален скорости и радиусу сферы (закон Стокса) .
Коэффициент пропорциональности в этом выражении имеет зависимость от свойств жидкости. Т.е., если шарик значимого веса бросить в высокий сосуд, содержащий вязкую жидкость (к примеру, глицерин), то спустя некоторое время скорость шарика установится на уровне определенного значения, не изменяющегося при последующем движении шарика. Когда движение будет происходить на некой установившейся скорости, силы, влияющие на шарик (сила тяжести
Навигация по статьям
