
Статью подготовили специалисты образовательного сервиса Zaochnik.
Основное уравнение МКТ газов. Температура
Содержание:
Модель идеального газа считается самой простейшей относительно основных положений МКТ. Кинетическая модель идеального газа молекул говорит о том, что при взаимодействии между собой, шарики рассматриваются в качестве идеально упругих. Суммарный объем всех молекул достаточно мал по сравнению с объемом сосуда, в котором находится данный газ. Модель необходима для описания его поведения при различных давлениях и температурах.
Цель молекулярно-кинетической теории – установка связи между макроскопическими и макроскопическими параметрами.
После соударения молекул между собой и стенками сосуда происходит изменение направления движения и времени между интервалами столкновений. Модель идеального газа основывается на законах механики Ньютона, то тесть столкновения соответствуют закону упругого удара.
Чтобы определить давление газа на стенку сосуда, учитывается модель идеального газа. Исходя из этого, происходит возникновение сил, которые подчиняются закону Ньютона. Отсюда получим, что проекция скорости перпендикулярна относительно стенки, а знак меняется на противоположный. Проекция параллельна и постоянна. Это показано на рисунке
Рисунок Упругое столкновение молекулы со стенкой.
Отсюда следует, что изменение импульса можно записать в виде с массой молекулы, равной . Необходимо выделить площадь , как показано на рисунке По прошествии времени с поверхностью столкнутся молекулы с проекциями скорости , которая направлена в сторону стены, и основанием цилиндра с высотой .
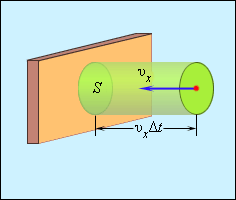
Рисунок Определение числа столкновений молекул с поверхностью .
Если за единицу объема брать сосуд с -ым количеством молекул, тогда их число в объеме цилиндра нужно обозначить, как . Очевидно, что происходит столкновение только половины имеющихся молекул. Тогда количество ударов о за время равняется .
При столкновении происходит изменение импульса . Тогда формула говорит о полном его изменении за определенный промежуток времени. Исходя из закона механики, изменение импульса всех молекул записывается как . Силой обозначается средняя сила, которая действует на молекулы. Но закон Ньютона говорит о том, что аналогичная сила по модулю оказывает действие на поверхность . Данное утверждение можно зафиксировать .
Далее для упрощения следует разделить равенство на выражение . Формула примет вид со значением , обозначаемым в качестве давления газа на стенку сосуда.
Все молекулы, находящиеся в сосуде на единицу объема, имеют разные проекции скоростей на ось . При столкновениях прослеживалось статистическое их распределение по скоростям, причем с разными направлениями векторов их скоростей.
Распределением Максвелла называют распределение молекул газа по модулю скоростей.
Еще в г Дж. Максвелл вывел закон распределения молекул газа по скоростям, основываясь на основных положениях молекулярно-кинетической теории молекулы. Рисунок наглядно показывает распределения молекул по скоростям с помощью кривых. На оси располагается модуль скорости, а на – количество молекул, находящихся на интервале от до . На рисунке данное значение выделено в виде столбика.
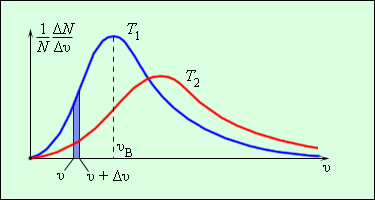
Рисунок Распределение молекул по скоростям. .
Характерные параметры распределения Максвелла – это вероятная скорость ,которая соответствует кривой распределения, и среднеквадратичная скорость , где обозначающие среднее значение квадрата скорости.
Если растет температура, тогда максимум кривой будет смещен в сторону больших скоростей, то есть и увеличатся.
Распределение Максвелла
Для записи формулы давления газа необходимо предположить, что все молекулы разделены на группы с проекциями . Иначе говоря, записываем . Можно зафиксировать, как . Тогда суммарное давление примет вид .
Данная сумма является суммой квадратов проекций всех молекул на единичном объеме газа. При делении выражения на получим среднее значение квадратичной скорости проекции . Запишем в виде .
Другая интерпретация формулы давления газа . Все направления векторов различные, потому среднее значение квадратов проекций на координатные оси равняется .
Формула для среднего давления газа на стенку сосуда обозначим, как .
Из уравнения видна связь между и и количеством молекул , средней квадратичной скоростью и средней кинетической энергией молекул. Такое уравнение получило название уравнения молекулярно-кинетической уравнения теории газов.
Отсюда следует, что давление газа – это две трети средней кинетической энергии, которое имеется в единице объема. Основное уравнение молекулярно-кинетической теории газов или строения вещества содержит произведение количества молекул на . Предположительно сосуд имеет газ неизменного объема , тогда ( - число молекул в сосуде). Изменение давления происходит пропорционально изменению кинетической энергии.
Физика. Температура
Температура связана с понятием теплового равновесия. При контакте тела обмениваются энергией, которая передается и получает название количества теплоты.
Тепловым равновесием называют состояние системы тел, которые находятся в тепловом контакте с теплопередачей и с постоянными макроскопическими параметрами.
Температура - физический параметр, который находится в тепловом равновесии. Введение понятия температуры идет из нулевого закона термодинамики.
Температура измеряется с помощью термометра. Для его создания выбирается термометрическое вещество и величину, которая его характеризует. Разные конструкции подразумевают отличия в их свойствах.
Каждый термометр должен быть откалиброван. Использование природных систем с неизменной температурой необходимо для хорошего теплообмена. Температура плавления льда равняется градусов Цельсия, а точка кипения воды – градусов. Одно маленькое деление из шкалы равняется градусу. Существует обозначение замерзания воды по Фаренгейту, то есть . Получаем, что формула примет вид или .
На рисунке изображен газовый термометр, который чаще всего заполняют разряженным гелием, воздухом с неизменным объемом, обозначаемым , и давлением . Из опыта видно, что возрастание давления идет с повышением температуры по Цельсию.

Рисунок Газовый термометр с постоянным объемом.
Температура кипения газов при давлении
Чтобы произвести калибровку газового термометра, следует выполнить измерение состояния молекул при и градусах. Для этого мы наносим точки и на график, после чего проводим прямую линию, как изображено на рисунке Получившийся калибровочный график способен определить температуру с разными значениями давления. При низких температурах возможно нахождение ее «гипотетической». Из опыта видно, что на свойства газа не влияет температура в. При понижении температур газ переходит в жидкое или твердое состояние, поэтому получение охлажденного газа невозможно.
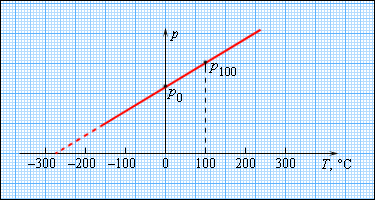
Рисунок Зависимость давления газа от температуры при .
В году У. Кельвин предлагает использовать точку нулевого давления газа для составления шкалы. Отличие от измерений температуры в Цельсиях в том, что нулевая точка сдвинута на .
По системе температура измеряется по Кельвину и обозначается . Тогда комнатная температура запишется , а по Кельвину – .
Температура кипения газов. Шкала Кельвина
Температурная шкала Кельвина считается абсолютной. Она наиболее приемлема для обозначения физических теорий.
Шкала Кельвина может быть не привязана двумя фиксированными точками, а именно: точка плавления льда и кипения воды с нормальным атмосферным давлением.
Нулевое давление называется абсолютным нулем температуры.
Шкала Кельвина имеет точку, в которой лед, вода и пар будут находиться в тепловом равновесии. Для калибровки других термометров применяют газовые, так как для практики они не подходят в виду своих больших размеров. Отсюда следует, что давление разреженного газа в сосуде постоянного объема изменяется прямо пропорционально его абсолютной температуре, то есть . Из опыта видно, что неизменный объем и температура давления прямо пропорциональны количеству вещества в сосуде к его объему: , где принимает обозначение числа молекул в сосуде, а – постоянная Авогадро, – концентрации молекул.
После объединения соотношений получим, что запись примет вид , где считается универсальной постоянной величиной для всех газов, иначе говоря, постоянная Больцмана. Этот ученый являлся одним из создателей опытного обоснования основных положений молекулярно-кинетической теории. Ее обозначение в системе .
При сравнении соотношения с уравнением МКТ газов, получим .
Средняя кинетическая энергия беспорядочного движения молекул газа прямо пропорциональна абсолютной температуре.
Температура является мерой для кинетической энергии молекул, которая не зависит от ее величины. Броуновская частица из жидкости и газа обладает аналогичной средней кинетической энергией, как и другая отдельная молекула. Это суждение верно для разномассовых молекул, находящихся в одном сосуде. Состояние равновесия говорит о том, что на них действуют одинаковые средние кинетические энергии, которые определяются температурой смеси. Запись давления смеси газов запишется как сумма парциальных давлений каждого из них: .
Отсюда видно, что является концентрацией молекул газов в смеси. Выражение относят к молекулярно-кинетической теории, установленной Дальтоном: давление в смеси химически невзаимодействующих газов равняется сумме их парциальных давлений.
Навигация по статьям
