
Статью подготовили специалисты образовательного сервиса Zaochnik.
Импульс тела
Содержание:
Если на тело массой m за определенный промежуток времени действует сила , тогда следует изменение скорости тела . Получаем, что за время тело продолжает движение с ускорением:
.
Основываясь на основном законе динамики, то есть втором законе Ньютона, имеем:
или .
Изменение импульса
Импульс тела, или количество движения – это физическая величина, равная произведению массы тела на скорость его движения.
Импульс тела считается векторной величиной, которая измеряется в килограмм-метр в секунду .
Импульс силы – это физическая величина, равняющаяся произведению силы на время ее действия.
Импульс относят к векторным величинам. Существует еще одна формулировка определения.
Изменение импульса тела равняется импульсу силы.
При обозначении импульса второй закон Ньютона записывается как:
.
Данный вид позволяет формулировать второй закон Ньютона. Сила является равнодействующей всех сил, действующих на тело. Равенство записывается как проекции на координатные оси вида:
.
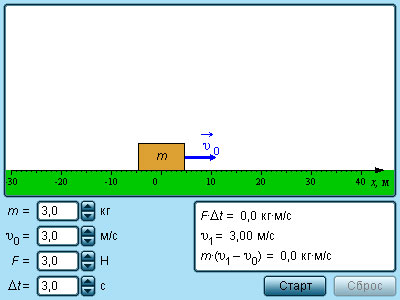
Рисунок Модель импульса тела.
Изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось.
Одномерное движение – это движение тела по одной из координатный осей.
На примере рассмотрим свободное падение тела с начальной скоростью под действием силы тяжести за промежуток времени . При направлении оси вертикально вниз импульс силы тяжести , действующий за время , равняется . Такой импульс равняется изменению импульса тела:
, откуда .
Запись совпадает с кинематической формулой определения скорости равноускоренного движения. По модулю сила не изменяется из всего интервала . Когда она изменяема по величине, тогда формула импульса требует подстановки среднего значения силы из временного промежутка . Рисунок показывает, каким образом определяется импульс силы, которая зависит от времени.
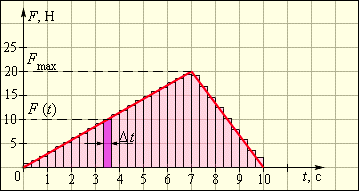
Рисунок Вычисление импульса силы по графику зависимости
Необходимо выбрать на временной оси интервал , видно, что сила практически неизменна. Импульс силы за промежуток времени будет равняться площади заштрихованной фигуры. При разделении временной оси на интервалы на на промежутке от от до , сложить импульсы всех действующих сил из этих промежутков , тогда суммарный импульс силы будет равняться площади образования при помощи ступенчатой и временной осей.
Применив предел , можно найти площадь, которая будет ограничиваться графиком и осью . Использование определения импульса силы по графику применимо с любыми законами, где имеются изменяющиеся силы и время. Данное решение ведет к интегрированию функции из интервала .
Рисунок показывает импульс силы, находящийся на интервале от с до .
Из формулы получим, что .
То есть, из примера видно .
Определение средней силы
Имеются случаи, когда определение средней силы возможно при известных времени и данных о сообщенном импульсе. При сильной ударе по мячу с массой можно сообщить скорость, равную . Приблизительным временем удара является значение .
Тогда формула импульса приобретает вид:
.
Чтобы определить среднюю силу во время удара, необходимо .
Получили очень большое значение, которое равняется телу массой .
Когда движение происходит по криволинейной траектории, то начальное значение и конечное
могут быть различны по модулю и по направлению. Для определения импульса применяют диаграмму импульсов, где имеются векторы и , а построен по правилу параллелограмма.
Для примера приводится рисунок , где нарисована схема импульсов мяча, отскакивающего от стены. При подаче мяч с массой со скоростью налетает на поверхность под углом α к нормали и отскакивает со скоростью с углом . При ударе в стену мяч подвергался действию силы , направленной также, как и вектор .
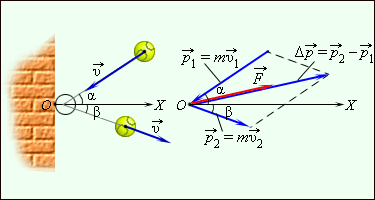
Рисунок Отскакивание мяча от шероховатой стенки и диаграмма импульсов.
Если происходит нормальное падение мяча с массой на упругую поверхность со скоростью , тогда при отскоке она изменится на . Значит, за определенный промежуток времени импульс изменится и будет равен . Используя проекции на , результат запишется как . Из рисунка видно, что ось направлена от стенки, тогда следует и . Из формулы получим, что модуль связан с модулем скорости, который принимает вид .
Навигация по статьям
