
Статью подготовили специалисты образовательного сервиса Zaochnik.
Энтропия идеального газа
Содержание:
В этой статье мы расскажем, что такое энтропия идеального газа и в чем заключается ее физический смысл. Начнем с определения.
Энтропия – это функция состояния системы с дифференциалом в бесконечном обратимом процессе, равным .
Параметр обозначает элементарное тепло, которое сообщается системе. Соответственно, – это общая температура системы.
Если у системы в обратимом процессе изменяется знак энтропии, то это говорит о смене направления обмена теплом. Основная формула дает нам возможность найти, на сколько изменилась величина энтропии. Важно подчеркнуть, что она будет верной только в том случае, если процесс будет обратим.
В чем состоит физический смысл энтропии
Свойства идеального газа таковы, что с их помощью удобно пояснять физический смысл энтропии. Допустим, у нас есть один моль некоторого газа, для которого мы можем записать первое правило термодинамики (в дифференциальной форме):
.
Выполним деление левой и правой части выражения на температуру. У нас получится, что:
.
Здесь . С помощью уравнения Менделеева-Клайперона мы можем выразить из него и получить:
.
Подставляем это в исходное выражение:
.
Правая часть уравнения у нас получилась полностью дифференциальной, значит, и слева тоже должен быть полный дифференциал. Назовем его . С помощью одной из приведенных выше формул вычислим в изотермическом процессе. Если температура остается постоянной, то и внутренняя энергия системы также остается прежней. Получаем следующее:
.
Нам известно, что объем, занимаемый газом в равновесном состоянии, связан с количеством пространственных микросостояний частиц формулой ( – общее количество микросостояний, – количество ячеек, в которые помещены частица системы, – общее количество частиц). Поскольку исходный объем идеального газа равен одному молю, то . Выведем формулу объемов и из выражения выше. Она будет иметь следующий вид:
.
Здесь .
Для дальнейших преобразований нам потребуется формула Стирлинга (для больших ):
.
Берем логарифм от этого выражения и получаем:
.
Таким образом, .
Здесь параметр обозначает постоянную Больцмана.
Формула Больцмана
Сам вид формулы энтропии говорит нам о том, что она может быть определена через логарифм числа микросостояний, образующих макросостояние, рассматриваемое как .
Выведенное выше равенство называется формулой Больцмана. Она позволяет сделать вывод, что чем больше упорядоченность системы, тем меньше в ней микросостояний, с помощью которых достигается макросостояние. Поэтому энтропия является мерой упорядоченности системы. Максимальная энтропия достигается в состоянии упорядоченности.
Энтропия является аддитивной величиной. При процесс называется изоэнтропийным. Если система является физически однородной, то ее энтропия выражается как функция двух независимых параметров состояния (масса считается постоянной).
Условие: есть идеальный газ, в котором происходит изотермическое расширение, при этом объем меняется от до . При этом температура системы в первом процессе равна , а во втором , причем вторая температура меньше, чем первая. Определите, как будет меняться значение энтропии.
Решение
Зная основное определение энтропии и обратимость процессов в идеальном газе, мы можем использовать формулу для вычисления при постоянной температуре.
.
Идеальный газ в физике – это понятие, подразумевающее, что мы можем пренебречь взаимодействием между его молекулами. Если , то работа идеального газа равна .
Обратимся к первому правилу термодинамики, зная, что при постоянной температуре :
.
Выражаем давление из уравнения Менделеева-Клайперона:
.
Подставляем в исходную формулу и получаем:
Ответ: поскольку не существует зависимости энтропии от температуры в изотермическом процессе, то в заданных условиях оба процесса будут иметь одинаковую энтропию.
Условие: на рисунке схематично обозначены обратимые процессы. Сопоставьте, какие количества теплоты будут поглощаться системой в ходе обеих процессов.
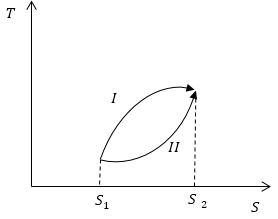
Решение
Данная задача решается на основе определения энтропии для обратимых процессов.
.
Выражаем показатель из уравнения, выведенного ранее, и получаем:
.
Для определения объема подведенного к системе тепла нам нужно проинтегрировать выражение:
.
Теперь, используя геометрическое свойство интеграла (по площади) и рисунок, мы можем подытожить, что площадь, ограниченная кривой процесса, изоэнтропами, перпендикулярными , и осью , больше площади для процесса , значит, .
Ответ: в первом процессе поглощается большее количество теплоты, чем в во втором.
Навигация по статьям
