Первый закон термодинамики

На рисунке $3.9.1$ условно проиллюстрированы энергетические потоки между выделенной термодинамической системой и окружающими телами. В случае, если тепловой поток направлен к термодинамической системе, то некоторая величина $Q>0$, если же система совершает положительную работу над окружающими ее объектами, то справедливо неравенство $A>0$.

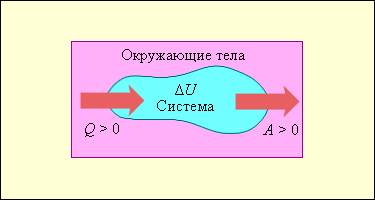
Рисунок $3.9.1.$ Обмен энергией между термодинамической системой и окружающими телами в результате теплообмена и совершаемой работы.

Состояние системы меняется, когда происходит процесс ее обмена теплом с окружающими объектами, и она совершает положительную или отрицательную работу. Изменяются макроскопические параметры системы, такие как температура, объем и давление. По причине того, что внутренняя энергия $U$ всецело определяется макроскопическими параметрами, которые характеризуют состояние системы, процессы совершения работы и теплообмена провоцируют изменения внутренней энергии данной системы $\Delta U$.

Определение $1$-го закона термодинамики

Первый закон термодинамики представляет собой некое обобщение закона сохранения и превращения энергии для термодинамической системы, и формулируется следующим образом:

$∆U=Q-A$.

Формула первого закона термодинамики, зачастую записывается в ином виде: 

$Q=∆U+A$.

Первый закон термодинамики представляет из себя, по сути, обобщение опытных фактов. Если руководствоваться им, то можно заявить, что энергия не возникает и не исчезает бесследно, а передается от одной системы к другой, меняя свои формы. Невозможность создания вечного двигателя (perpetuum mobile) первого рода, то есть машины, которая может совершать полезную работу, не потребляя энергию извне и не претерпевая каких-либо изменений во внутренней конструкции агрегата, являлась важным следствием первого закона термодинамики. В подтверждение этого выступает тот факт, что каждая из огромного множества попыток создания такого устройства неизменно заканчивалась неудачей. Реальная машина может совершать положительную работу $A$ над внешними объектами, только получая некоторое количество теплоты $Q$ от окружающих тел или уменьшая $\Delta U$ своей внутренней энергии.

Первый закон термодинамики в процессах газов

Первый закон термодинамики может применяться к изопроцессам в газах.

В этом случае справедливой будет формула внутренней энергии газа:

$Q=∆U=U\left(T_2\right)-U\left(T_1\right)$.

В данном выражении $U\left(T_1\right)$ и $U\left(T_2\right)$ представляют внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит лишь от температуры, что исходит из закона Джоуля. При изохорном нагревании газ поглощает тепло $(Q>0)$, чем провоцирует увеличение его внутренней энергии. В условиях охлаждения тепло отдается внешним объектам $(Q<0)$.

Первый закон термодинамики для изобарного процесса дает: 

$Q=U\left(T_2\right)-U\left(T_1\right)+p(V_2-V_1)=∆U+p∆V$.

При изобарном расширении $Q>0$ тепло поглощается газом, и он совершает положительную работу. При изобарном сжатии $Q<0$ тепло переходит внешним телам. В таком случае $A<0$. При изобарном сжатии уменьшаются температура газа $T_2<T_1$ и значение внутренней энергии $\Delta U<0$.

Первый закон термодинамики для изотермического процесса выражается соотношением 

$Q=A$

Теплота $Q$, приобретенная газом в процессе изотермического расширения, превращается в работу, совершаемую над внешними объектами. И наоборот, изотермическое сжатие приводит к преобразованию уже работы внешних сил, произведенной над газом, в передающееся окружающим телам тепло.

Вместе с изохорным, изотермическим и изобарным процессами в термодинамике нередко исследуют процессы, происходящие в условиях отсутствующего теплообмена с окружающими объектами.

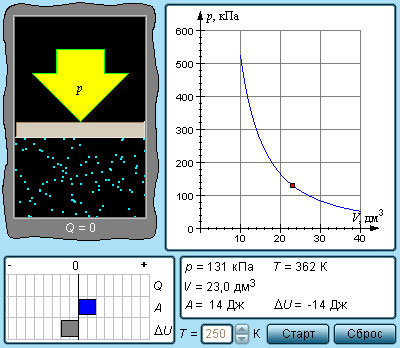
Рисунок $3.9.2.$ Модель адиабатического процесса.

Выходит, что газ производит работу за счет падения значения его внутренней энергии.

В процессе адиабатического расширения газом совершается положительная работа $A>0$, что является причиной понижения значения внутренней энергии $\Delta U<0$. Данное явление провоцирует падение его температуры. Исходя из этого, можно заявить, что величина давления газа при адиабатическом расширении понижается быстрее, чем это происходит в изотермическом (рис. $3.9.3$).

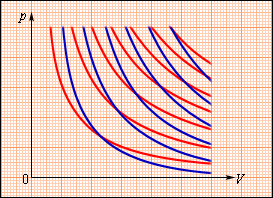
Рисунок $3.9.3.$ Семейства изотерм (красные кривые) и адиабат (синие кривые) идеального газа.

В условиях координат $(p, V)$ выводящееся в термодинамике уравнение адиабатического процесса для идеального газа принимает следующий вид: 

$p{V}^{\gamma }=const$.

Данное выражение, в котором $\gamma =\frac{C_p}{C_V}$ – показатель адиабаты, $C_p$ и $C_V$ – теплоемкости газа в процессах с постоянным давлением и с постоянным объемом, называется уравнением Пуассона. В условиях одноатомного газа $\gamma =\frac{5}{3}=1,67$, двухатомного $\gamma =\frac{7}{5}=1,4$, многоатомного $\gamma =1,33$.

Работа газа в адиабатическом процессе выражается через температуры начального $T_1$ и конечного $T_2$ состояний и принимает вид: 

$A=C_V(T_2-T_1)$

Адиабатический процесс относится к изопроцессам.

В термодинамике важное место занимает физическая величина, называемая энтропией. Изменение энтропии в том или ином квазистатическом процессе эквивалентно некоторому обретенному системой теплу $\frac{\Delta Q}{T}$. Так как на каждом участке адиабатического процесса $\Delta Q=0$, энтропия в нем не претерпевает изменений.

Любые изопроцессы, в том числе и адиабатические, являются квазистатическими. Промежуточные состояния газа в таких процессах близки к состояниям термодинамического равновесия. Каждая точка, принадлежащая адиабате, описывает равновесное состояние. Однако, процесс, который проводится в адиабатической оболочке, то есть при отсутствующем теплообмене с окружающими объектами, не обязательно удовлетворяет данному условию.

В таком процессе $Q=0$, по той причине, что исключен теплообмен с окружающими телами, и $A=0$, так как оболочка недеформируема. Первый закон термодинамики позволяет сказать, что $\Delta U=0$, то есть внутренняя энергия газа не претерпела никаких изменений. Так как внутренняя энергия идеального газа зависит лишь от температуры, температура газа в начальном и конечном состояниях одинакова. Изображающие эти состояния точки на плоскости $(p, V)$ лежат на одной изотерме. Все промежуточные состояния газа не являются равновесными и не могут быть изображены на диаграмме.

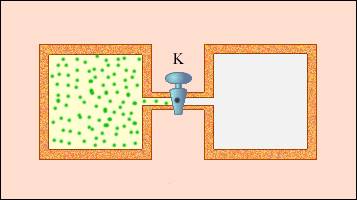
Рисунок $3.9.4.$ Расширение газа в пустоту.