Сила Лоренца

Сила Лоренца. Определение и формула

Пускай заряд носителя обозначается как $q$, а $n$ является значением концентрации носителей свободного заряда в проводнике. В этом случае произведение $n·q·\upsilon ·S$, в котором $S$ представляет собой площадь поперечного сечения проводника, эквивалентно току, протекающему в проводнике, а $\upsilon$ – это модуль скорости упорядоченного движения носителей в проводнике:

$I=q·n·\upsilon ·S$.

Направление силы Лоренца, которая воздействует частицу с положительным зарядом, таким же образом, как и направление силы Ампера, находится по правилу буравчика или же с помощью правила левой руки. Взаимное расположение векторов $\overrightarrow{\nu }, \overrightarrow{B}$ и $\overrightarrow{F_{Л}}$ для частицы, несущей положительный заряд, проиллюстрировано на рис. $1.18.1$.

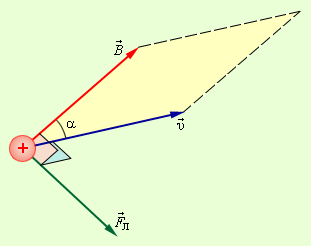
Рисунок $1.18.1.$ Взаимное расположение векторов $\overrightarrow{\nu }, \overrightarrow{B}$ и $\overrightarrow{F_{Л}}$. Модуль силы Лоренца $\overrightarrow{F_{Л}}$ численно эквивалентен произведению площади параллелограмма, построенного на векторах $\overrightarrow{\nu }$ и $\overrightarrow{B}$ и заряда $q$.

Сила Лоренца направлена нормально, то есть перпендикулярно, векторам $\overrightarrow{\nu }$ и $\overrightarrow{B}$.

Сила Лоренца не совершает работы при движении несущей заряд частицы в магнитном поле. Данный факт приводит к тому, что модуль вектора скорости в условиях движения частицы так же не меняет своего значения.

Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость $\overrightarrow{\nu }$ лежит в плоскости, которая направлена нормально по отношению к вектору $\overrightarrow{B}$, то частица будет совершать движение по окружности некоторого радиуса, рассчитывающегося с помощью следующей формулы:

$R=\frac{m\nu }{qB}$.

Сила Лоренца в данном случае применяется в качестве центростремительной силы (рис. $1.18.2$).

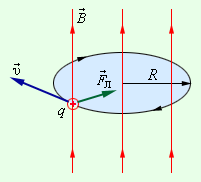
Рисунок $1.18.2.$ Круговое движение заряженной частицы в однородном магнитном поле.

Для периода обращения частицы в однородном магнитном поле будет справедливо следующее выражение:

$T=\frac{2\pi R}{\upsilon }=\frac{2\pi m}{qB}$.

Данная формула наглядно демонстрирует отсутствие зависимости заряженных частиц заданной массы $m$ от скорости $\upsilon$ и радиуса траектории $R$.

Применение силы Лоренца

На рисунке $1.18.3$ приводится принципиальная схема циклотрона.

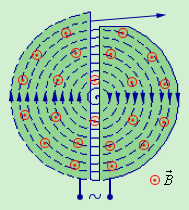
Рисунок $1.18.3.$ Движение заряженных частиц в вакуумной камере циклотрона.

К дуантам приложено переменное электрическое напряжение, чья частота эквивалентна циклотронной частоте. Частицы, несущие некоторый заряд, инжектируются в центре вакуумной камеры. В промежутке между дуантами они испытывают ускорение, вызываемое электрическим полем. Частицы, находящиеся внутри дуантов, в процессе движения по полуокружностям испытывают на себе действие силы Лоренца. Радиус полуокружностей возрастает с увеличением энергии частиц. Как и во всех других ускорителях, в циклотронах ускорение заряженной частицы достигается путем применения электрического поля, а ее удержание на траектории с помощью магнитного поля. Циклотроны дают возможность ускорять протоны до энергии, приближенной к $20 МэВ$.

Однородные магнитные поля используются во многих устройствах самых разных типов назначений. В частности, они нашли свое применение так называемых масс-спектрометрах.

Данные приборы используются для разделения изотопов (ядер атомов с одинаковым зарядом, но разными массами, к примеру, ${}^{20}\mathrm{Ne}$ и ${}^{22}\mathrm{Ne}$). На рис. $1.18.4$ изображен простейшая версия масс-спектрометра. Вылетающие из источника $S$ ионы проходят через несколько малых отверстий, которые в совокупности формируют узкий пучок. После этого они попадают в селектор скоростей, где частицы движутся в скрещенных однородных электрическом, создающимся между пластинами плоского конденсатора, и магнитном, возникающим в зазоре между полюсами электромагнита, полях. Начальная скорость $\overrightarrow{\upsilon }$ заряженных частиц направлена перпендикулярно векторам $\overrightarrow{E}$ и $\overrightarrow{B}$.

Частица, которая движется в скрещенных магнитном и электрическом полях, испытывает на себе воздействия электрической силы $q\overrightarrow{E}$ и магнитной силы Лоренца. В условиях, когда выполняется $E=\upsilon B$, данные силы полностью компенсируют воздействие друг друга. В таком случае частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, которые движутся со скоростью $\upsilon =\frac{E}{B}$.

После данных процессов частицы с одинаковыми значениями скорости попадают в однородное магнитное поле $\overrightarrow{B}$ камеры масс-спектрометра. Частицы под действием силы Лоренца движутся в камере перпендикулярной магнитному полю плоскости. Их траектории представляют собой окружности с радиусами $R=\frac{m\upsilon }{qB\text{'}}$. В процессе измерения радиусов траекторий при известных значениях $\upsilon$ и $B\text{'}$, мы имеем возможность определить отношение $\frac{q}{m}$. В случае изотопов, то есть при условии $q_1=q_2$, масс-спектрометр может разделить частицы с разными массами.

С помощью современных масс-спектрометров мы имеем возможность измерять массы заряженных частиц с точностью, превышающей ${10}^{–4}$.

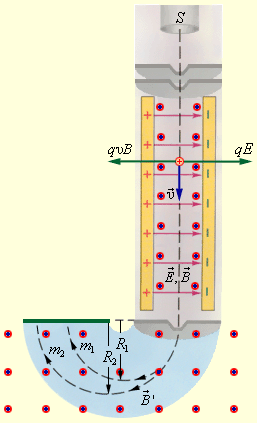
Рисунок $1.18.4.$ Селектор скоростей и масс-спектрометр.

Магнитное поле

В случае, когда скорость частицы $\overrightarrow{\upsilon }$ имеет составляющую $\overrightarrow{{\upsilon }_{\parallel }}$ вдоль направления магнитного поля, подобная частица в однородном магнитном поле будет совершать спиралевидное движение. Радиус такой спирали $R$ зависит от модуля перпендикулярной магнитному полю составляющей $\upsilon ┴$ вектор $\overrightarrow{\upsilon }$, а шаг спирали $p$ – от модуля продольной составляющей ${\upsilon }_{\parallel }$ (рис. $1.18.5$).

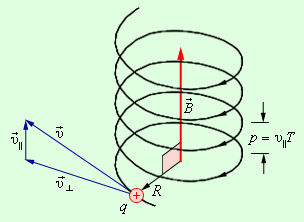
Рисунок $1.18.5.$ Движение заряженной частицы по спирали в однородном магнитном поле.

Исходя из этого, можно сказать, что траектория заряженной частицы в каком-то смысле «навивается» на линии магнитной индукции. Данное явление используется в технике для магнитной термоизоляции высокотемпературной плазмы - полностью ионизированного газа при температуре порядка ${10}^6 K$. При изучении управляемых термоядерных реакций вещество в подобном состоянии получают в установках типа «Токамак». Плазма не должна касаться стенок камеры. Термоизоляция достигается путем создания магнитного поля специальной конфигурации. На рисунке $1.18.6$ в качестве примера проиллюстрирована траектория движения несущей заряд частицы в магнитной «бутылке» (или ловушке).

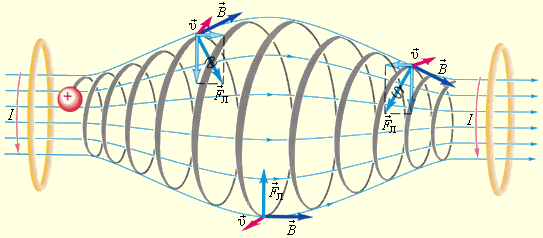
Рисунок $1.18.6.$ Магнитная «бутылка». Заряженные частицы не выходят за ее пределы. Необходимое магнитное поле может быть создано с помощью двух круглых катушек с током.

Такое же явление происходит в магнитном поле Земли, которое защищает все живое от потока несущих заряд частиц из космического пространства.

Исключением являются полярные области, в которых часть частиц прорывается в верхние слои атмосферы, что может приводить к возникновению таких явлений, как «полярные сияния». Радиационные пояса Земли простираются от расстояний около $500 км$ до десятков радиусов нашей планеты. Стоит вспомнить, что южный магнитный полюс Земли находится поблизости с северным географическим полюсом на северо-западе Гренландии. Природа земного магнетизма до сих пор не изучена.

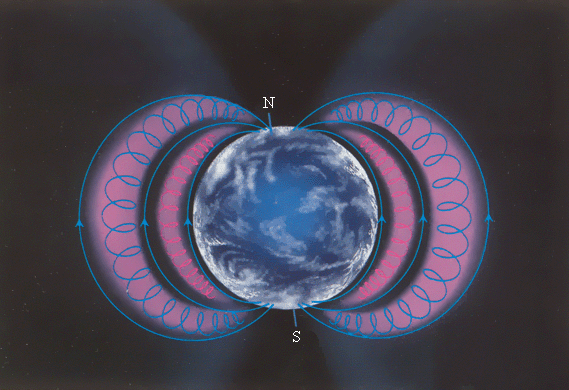
Рисунок $1.18.7.$ Радиационные пояса Земли. Быстрые заряженные частицы от Солнца, в основном электроны и протоны, попадают в магнитные ловушки радиационных поясов.

Возможно их вторжение в верхние слои атмосферы, служащее причиной возникновения «северных сияний».

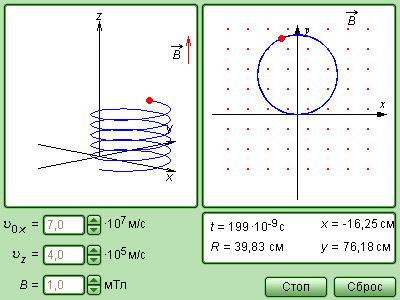
Рисунок $1.18.8.$ Модель движения заряда в магнитном поле.

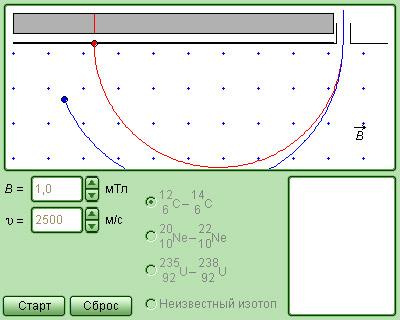
Рисунок $1.18.9.$ Модель Масс-спектрометра.

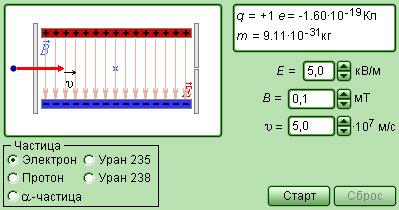
Рисунок $1.18.10.$ Модель селектора скоростей.