
Статью подготовили специалисты образовательного сервиса Zaochnik.
Линейные неравенства, примеры, решения
Содержание:
После получения начальных сведений о неравенствах с переменными, переходим к вопросу их решения. Разберем решение линейных неравенств с одной переменной и все методы для их разрешения с алгоритмами и примерами. Будут рассмотрены только линейные уравнения с одной переменной.
Что такое линейное неравенство?
В начале необходимо определить линейное уравнение и выяснить его стандартный вид и чем оно будет отличаться от других. Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.
Линейное неравенство с одной переменной – это неравенство вида , когда вместо используется любой знак неравенства и являются действительными числами, где .
Неравенства или , с являющимся переменной, а и некоторыми числами, называют линейными неравенствами с одной переменной.
Так как ничего не сказано за то, может ли коэффициент быть равным , тогда строгое неравенство вида и может быть записано в виде нестрогого, а именно, , . Такое уравнение считается линейным.
Их различия заключаются в:
- форме записи в первом, и – во втором;
- допустимости равенства нулю коэффициента , - в первом, и - во втором.
Считается, что неравенства и равносильные, потому как получены переносом слагаемого из одной части в другую. Решение неравенства приведет к тому, что его необходимо будет решить, причем случай не подойдет.
Считается, что линейными неравенствами в одной переменной считаются неравенства вида и , где и являются действительными числами. Вместо может быть обычное число.
Исходя из правила, имеем, что являются примерами линейных неравенств. А неравенства такого плана, как называют сводящимися к линейному.
Как решить линейное неравенство
Основным способом решения таких неравенств сводится к равносильным преобразованиям для того, чтобы найти элементарные неравенства являющееся некоторым числом, при , а вида при .
Для решения неравенства с одной переменной, можно применять метода интервалов или изображать графически. Любой из них можно применять обособленно.
Используя равносильные преобразования
Чтобы решить линейное неравенство вида , необходимо применить равносильные преобразования неравенства. Коэффициент может быть равен или не равен нулю. Рассмотрим оба случая. Для выяснения необходимо придерживаться схемы, состоящей из пунктов: суть процесса, алгоритм, само решение.
Алгоритм решение линейного неравенства при
- число будет перенесено в правую часть неравенства с противоположным знаком, что позволит прийти к равносильному ;
- будет производиться деление обеих частей неравенства на число не равное . Причем , когда является положительным, то знак остается, когда – отрицательное, меняется на противоположный.
Рассмотрим применение данного алгоритма на решении примеров.
Решить неравенство вида .
Решение
Данное линейное неравенство имеет и . Значит, коэффициент при не равен нулю. Применим выше сказанные алгоритмы, решим.
Необходимо перенести слагаемое в другую часть неравенства с изменением знака перед ним. Тогда получаем неравенство вида . Необходимо произвести деление обеих частей на . Знак не поменяется, так как является положительным числом. Получаем, что , что даст результат .
Неравенство вида является равносильным. То есть решение для – это любое действительное число, которое меньше или равно . Ответ записывается в виде неравенства , или числового промежутка вида .
Весь выше прописанный алгоритм записывается так:
Ответ: или .
Указать все имеющиеся решения неравенства .
Решение
Из условия видим, что коэффициент при равняется , а в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.
Производим деление обеих частей уравнения на число . Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что , и дальше .
Весь алгоритм запишем в краткой форме:
Ответ: или.
Решить неравенство .
Решение
По условию видим, что необходимо решить неравенство с коэффициентом при переменной , которое равняется , с коэффициентом , которому соответствует дробь . Решать неравенство необходимо, следуя алгоритму, то есть: перенести в другую часть с противоположным знаком, разделить обе части на , изменить знак неравенства:
При последнем переходе для правой части используется правило деления числе с разными знаками , после чего выполняем деление обыкновенной дроби на натурально число .
Ответ: и .
Рассмотрим случай, когда . Линейное выражение вида является неравенством , где на рассмотрение берется неравенство вида , после чего выясняется, оно верное или нет.
Все основывается на определении решения неравенства. При любом значении получаем числовое неравенство вида , потому что при подстановке любого вместо переменной , тогда получаем , где . В случае, если оно верно, то для его решения подходит любое значение. Когда неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.
Все суждения рассмотрим в виде алгоритма решения линейных неравенств :
Числовое неравенство вида верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.
Решить неравенство .
Решение
Данное линейное неравенство может принимать любое значение . Тогда получим неравенство вида . Последнее неравенство считается верным, значит любое число может быть его решением.
Ответ: промежуток .
Найти решение неравенства .
Решение
При подстановке переменной любого числа получим, что неравенство получит вид −. Оно является неверным. То есть не имеет решений.
Ответ: решений нет.
Рассмотрим решение линейных неравенств , где оба коэффициента равняется нулю.
Определить не имеющее решение неравенство из и .
Решение
При подстановке любого числа вместо получим два неравенства вида и . Первое является неверным. Значит, не имеет решений, а имеет бесконечное количество решений, то есть любое число.
Ответ: неравенство не имеет решений, а имеет решения.
Методом интервалов
Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.
Метод интервалов применяется для линейных неравенств при значении коэффициента не равному . Иначе придется вычислять при помощи другого метода.
Метод интервалов – это:
- введение функции ;
- поиск нулей для разбивания области определения на промежутки;
- определение знаков для понятия их на промежутках.
Соберем алгоритм для решения линейных уравнений при с помощью метода интервалов:
- нахождение нулей функции , чтобы решить уравнение вида . Если , тогда решением будет единственный корень, который примет обозначение ;
- построение координатной прямой с изображением точки с координатой , при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
- определение знаков функции на промежутках, для этого необходимо находить значения функции в точках на промежутке;
- решение неравенства со знаками или на координатной прямой добавляется штриховка над положительным промежутком, или над отрицательным промежутком.
Рассмотрим несколько примеров решения линейного неравенства при помощи метода интервалов.
Решить неравенство .
Решение
Из алгоритма следует, что для начала нужно найти корень уравнения . Получаем, что . Необходимо изобразить координатную прямую, где отмечаем точку . Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.
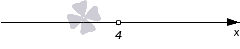
Нужно определить знаки на промежутках. Чтобы определить его на промежутке , необходимо произвести вычисление функции при . Отсюда получим, что . Знак на промежутке является положительным.
Определяем знак из промежутка , тогда подставляем значение . Имеем, что . Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.
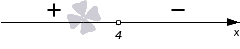
Мы выполняем решение неравенства со знаком , причем штриховка выполняется над положительным промежутком. Рассмотрим чертеж, приведенный ниже.
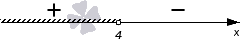
Из чертежа видно, что искомое решение имеет вид или .
Ответ: или .
Графическим способом
Чтобы понять, как изображать графически, необходимо рассмотреть на примере линейных неравенства: и . Их решениями будут значения и . Для этого изобразим график линейной функции , приведенный ниже.
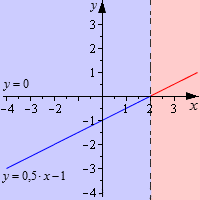
Видно, что
- решением неравенства считается промежуток, где график функции располагается ниже ;
- решением считается промежуток, где функция ниже или совпадает;
- решением считается промежуток, гре функция располагается выше ;
- решением считается промежуток, где график выше или совпадает.
Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике. В данном случае получаем, что левая часть имеет , а правая – , причем совпадает с .
Алгоритм решения линейных неравенств графическим способом.
Построение графика функции производится:
- во время решения неравенства определяется промежуток, где график изображен ниже ;
- во время решения неравенства определяется промежуток, где график изображается ниже оси или совпадает;
- во время решения неравенства производится определение промежутка, где график изображается выше ;
- во время решения неравенства производится определение промежутка, где график находится выше или совпадает.
Решить неравенство при помощи графика.
Решение
Необходимо построить график линейной функции . Данная прямая является убывающей, потому как коэффициент при является отрицательным. Для определения координат точки его пересечения с получим значение . Изобразим графически.
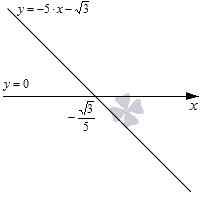
Решение неравенства со знаком , тогда необходимо обратить внимание на промежуток выше . Выделим красным цветом необходимую часть плоскости и получим, что
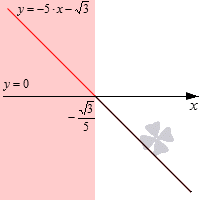
Необходимый промежуток является частью красного цвета. Значит, открытый числовой луч будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки также являлось бы решением неравенства. И совпадало бы с .
Ответ: или .
Графический способ решения используется, когда левая часть будет отвечать функции , то есть . Тогда прямая будет параллельна или совпадающей при . Эти случаю показывают, что неравенство может не иметь решений, либо решением может быть любое число.
Определить из неравенств , то, которое имеет хотя бы одно решение.
Решение
Представление является , тогда будет задана координатная плоскость с прямой, параллельной и находящейся выше . Значит, решений не имеет, потому как нет промежутков.
График функции , считается , то есть прямая совпадает с . Значит, неравенство имеет множество решений.
Ответ: второе неравенство имеет решение при любом значении .
Неравенства, сводящиеся к линейным
Решение неравенств можно свести к решению линейного уравнения, которые называют неравенствами, сводящимися к линейным.
Данные неравенства были рассмотрены в школьном курсе, так как они являлись частным случаем решения неравенств, что приводило к раскрытию скобок и приведению подобных слагаемых. Для примера рассмотрим, что .
Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.
При сведении неравенства к линейному, представляем его таким образом, чтобы оно имело вид , а для приведения второго получаем, что . Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
Это приводит решение к линейному неравенству.
Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.
Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:
- раскрыть скобки;
- слева собрать переменные, а справа числа;
- привести подобные слагаемые;
- разделить обе части на коэффициент при .
Решить неравенство .
Решение
Производим раскрытие скобок, тогда получим неравенство вида . После приведения подобных слагаемых имеем, что . После перенесения слагаемых с левой в правую, получим, что . Отсюда имеет неравенство вида из полученного при вычислении . Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Ответ: нет решений.
Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, является показательным уравнением, которое сводится к решению линейного вида . Эти случаи будут рассмотрены при решении неравенств данного вида.
Навигация по статьям
