Вынужденные колебания. Резонанс. Автоколебания

Если колебания совершаются под воздействием внешней силы, они называются вынужденными. Работа внешней силы, которая обеспечивает колебательную систему энергией, при этом является положительной. Благодаря ей колебания не затухают и могут противодействовать силам трения.

Внешняя сила не обязательно должна быть постоянной. С течением времени она может изменяться по разным законам. Особый случай – воздействие на колебательную систему внешней силы, которая изменяется по гармоническому закону с частотой, равной $\omega$, в то время как сама система совершает собственные колебания с той же самой частотой.

Когда внешняя сила начинает воздействовать на колебательную систему, должно пройти некоторое время $\Delta t$ , прежде чем вынужденные колебания установятся. Это время будет равно тому времени $\tau$, за которое затухают свободные колебания в данной системе.

В момент начала воздействия в системе начинают происходить два процесса одновременно – свободные колебания с собственной частотой ${\omega }_0$ и вынужденные с частотой $\omega$. Однако из-за сил трения свободные колебания в определенный момент затухают, поэтому по прошествии времени в системе сохраняются лишь стационарные колебания с той частотой, которая соответствует внешней (вынуждающей) силе.

Перемещения такого рода обеспечиваются шатунным механизмом, который преобразует круговые движения в возвратно-поступательные.

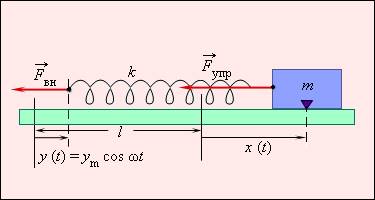
Рисунок $2.5.1.$ Груз на пружине, совершающий вынужденные колебания. Перемещение свободного конца выражено формулой $y=y_m \cos \omega t$, где $l$ означает длину недеформированной пружины, а $k$ –ее жесткость.

При смещении левого конца пружины на некоторое расстояние y и правого – на $x$ по сравнению с первоначальным положением недеформированной пружины будет происходить ее удлинение. Найти величину этого удлинения можно по следующей формуле:

$∆l=x-y=x-y_m\cos \omega t$.

В таком случае мы можем переформулировать второй закон Ньютона для этого случая следующим образом:

$ma=-k(x-y)=-kx+k{y}_m\cos \omega t$.

Здесь сила, которая действует на тело, показана как сумма двух слагаемых, первым из которых является упругость, стремящаяся к равновесию тела, а вторым – внешнее воздействие, совершающееся с определенными интервалами. Внешнюю силу также называют вынуждающей.

Теперь выразим эту зависимость в строгой математической формуле, учитывающей связь между координатой тела $a=\ddot{x}$  и его ускорением. У нас получится следующее:

$\ddot{x}+{\omega }_0^{2}x=A \cos \omega t$.

Эта зависимость называется уравнением внешних колебаний. Здесь ${\omega }_0=\sqrt{\frac{k}{m}}$ является собственной круговой частотой свободного колебания, а $\omega$ – циклической частотой внешней (вынуждающей) силы.

Чтобы найти величину $A$ для вынужденного колебания груза на пружине, нужно воспользоваться следующей формулой:

$A=\frac{k}{m}{y}_m-{\omega }_0^2{y}_m$.

То уравнение, что мы записали перед этим, не учитывает, что на тело действуют также и силы трения. В уравнении вынужденных колебаний, в отличие от уравнения свободных, учитываются сразу обе частоты – частота вынуждающей силы и частота свободных колебаний.

Вынужденные колебания груза на пружине, которые устанавливаются со временем, имеют частоту внешнего воздействия. Это определяется следующим законом:

$x\left(t\right)=x_m\cos (\omega t+\theta )$.

Здесь $x_m$ обозначает амплитуду вынужденного колебания, а буква $\theta$ – его начальную фазу. Значения обоих этих показателей будут зависеть от амплитуды внешней силы и соотношения частот.

Если частоты очень низкие, т.е. $\omega \ll \omega 0$, то тело, прикрепленное к правому концу пружины, движется точно так же, как и левый конец этой пружины. Тогда получается, что $x\left(t\right)=y\left(t\right)$. Сама пружина при этом практически не деформируется, а модуль внешней силы ${\overrightarrow{F}}_{вн}$, приложенной к ее левому концу, стремится к нулю. Работа при этом не совершается.

Понятие резонанса

С помощью резонансной кривой (резонансной характеристики) можно описать зависимость, существующую между амплитудой внешних колебаний $x_m$ и частотой вынуждающей силы $\omega$.

Когда происходит резонанс, амплитуда $x_m$ может оказаться значительно больше, чем амплитуда колебаний левого (свободного) конца пружины.. Если мы не будем учитывать силы трения, то получится, что при резонансной частоте амплитуда вынужденных колебаний будет возрастать неограниченно. В реальности она будет зависеть от следующего условия: работа внешней силы в течение всего времени колебаний должна совпадать с потерями механической энергии, происходящими из-за трения. При уменьшении трения (и, соответственно, повышении добротности $Q$ колебательной системы) амплитуда вынужденных колебаний при резонансе возрастет.

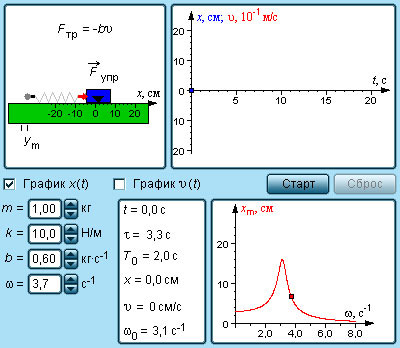
Рисунок $2.5.2.$ Моделирование вынужденных колебаний.

Если добротность колебательной системы невысока (менее $10$), то частота резонанса будет находиться ближе к низким частотам. Это показано на иллюстрации $2.5.2.$

Явление резонанса имеет большое практическое значение. Именно из-за него зачастую разрушаются здания, мосты и другие сооружения. Это происходит в тот момент, когда их собственные частоты совпадают с частотой внешней силы, например, колебаниями мотора.

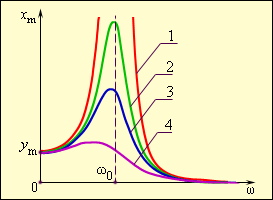
Рисунок $2.5.3.$ Изображение затухания различных колебаний при помощи резонансных кривых: $1$ - условная система без учета трения (бесконечное возрастание амплитуды вынужденных колебаний), $2,3,4$ – резонансные колебания в реальных условиях, происходящих в системах разной степени добротности $(Q_2>Q_3>Q_4)$. Если частоты низкие, то $(\omega \ll {\omega }_0) x_m\approx y_m$, а если высокие, то $(\omega \gg \omega 0) x_m\to 0$.

Вынужденные колебания являются незатухающими. При трении неизбежно теряется часть энергии, однако воздействие внешних периодически действующих сил компенсирует ее.

Что такое автоколебательные системы

Внутри этой системы можно выделить три составляющих – саму систему, источник внешней постоянной энергии и обратную связь между ними. Первым элементом выступает любая механическая система, которая может совершать затухающие колебания, например, часовой маятник. В качестве источника можно использовать потенциальную энергию груза в поле тяжести или энергию деформации пружины. Система обратной связи – это, как правило, особый механизм, функцией которого является регулирование поступлений энергии. На иллюстрации показано, как эти компоненты взаимодействуют между собой.

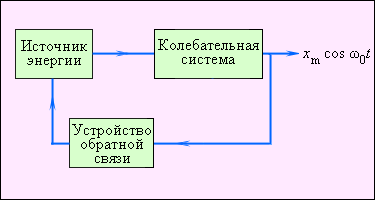
Рисунок $2.5.4.$ Автоколебательная система со всеми основными составляющими.

Какие можно привести примеры таких систем? Ярким примером является часовой механизм с так называемым анкерным ходом. В нем есть ходовое колесо с косыми зубчиками, прочно сцепленное с зубчатым барабаном, через который перекинута цепочка с грузом. В верхней части маятника закреплен якорек (анкер), состоящий из двух твердых пластинок, дугообразно изогнутых по окружности с центром на основной оси. В механизме ручных часов вместо гири используется пружина, а вместо маятника – маховичок-балансир, соединенный со спиральной пружиной, который совершает круговые колебания вокруг своей оси. В качестве источника внешней энергии выступает заведенная пружина или поднятая гиря. Обратная связь осуществляется с помощью анкера: он позволяет ходовому колесу совершать поворот только на один зубец за полупериод. Когда анкер взаимодействует с ходовым колесом, происходит передача энергии. Когда маятник колеблется, зубец ходового колеса передает анкерной вилке энергию по направлению движения маятника, и именно этим компенсируются силы трения. Таким образом, энергия поднятой гири или заведенной пружины поступает маленькими порциями к маятнику.

Существует также много других автоколебательных систем, которые широко применяются в технике. Автоколебания происходят внутри двигателей внутреннего сгорания, паровых машин, электрических звонков, музыкальных инструментов, голосовых связок и т.д.

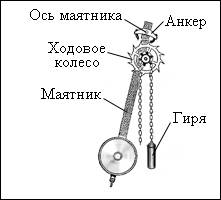
Рисунок $2.5.5.$ Схема маятникового часового механизма.