
Статью подготовили специалисты образовательного сервиса Zaochnik.
Свободные колебания. Пружинный маятник
Содержание:
Свободные колебания могут совершаться под действием внутренних сил только после выведения из положения равновесия всей системы.
Чтобы колебания совершались согласно гармоническому закону, нужно, чтобы сила, возвращающая тело в положение равновесия, была пропорциональна смещению тела из равновесного положения и направлена в сторону, противоположную смещению.
.
Соотношение говорит о том, что является частотой гармонического колебания. Данное свойство характерно для упругой силы в пределах применимости закона Гука:
.
Силы любой природы, которые удовлетворяют условию, называют квазиупругими.
То есть груз с массой , прикрепляющийся к пружине жесткости с неподвижным концом, изображенным на рисунке , составляют систему, способную совершать гармонические свободные колебания при отсутствии силы трения.
Груз, располагаемый на пружине, называют линейным гармоническим осциллятором.
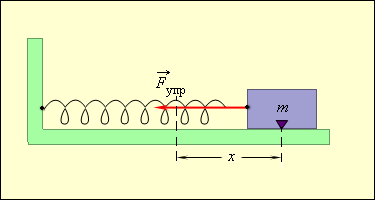
Рисунок Колебания груза на пружине. Трения нет.
Круговая частота
Нахождение круговой частоты производится с помощью применения формулы второго закона Ньютона:
.
Значит, получаем:
.
Частоту называют собственной частотой колебательной системы.
Определение периода гармонических колебаний груза на пружине находится из формулы:
.
Горизонтальное расположение системы пружина-груз, сила тяжести компенсируется силой реакции опоры. При подвешивании груза на пружину направление силы тяжести идет по линии движения груза. Положение равновесия растянутой пружины равняется:
, тогда как колебания выполняются около нового равновесного состояния. Формулы собственной частоты и периода колебаний в вышеуказанных выражениях являются справедливыми.
При имеющейся математической связи между ускорением тела и координатой поведение колебательной системы характеризуется строгим описанием: ускорение является второй производной координаты тела по времени :
.
Описание второго закона Ньютона с грузом на пружине запишется как:
, или , где свободная частота .
Если физические системы зависят от формулы , тогда они в состоянии совершать свободные колебательные гармонические движения с различной амплитудой. Это возможно, так как применяется .
Свободные колебания
Уравнение вида получило название уравнения свободных колебаний. Их физические свойства могут определять только собственную частоту колебаний или период .
Амплитуда и начальная фаза находят при помощи способа, который вывел их из состояния равновесия начального момента времени.
При наличии смещенного груза из положения равновесия на расстояние и моменте времени, равном , производится его опускание без начальной скорости. Тогда . Если груз находился в положении равновесия, то при толчке передается начальная скорость , отсюда .
Амплитуда с начальной фазой определяются наличием начальных условий.
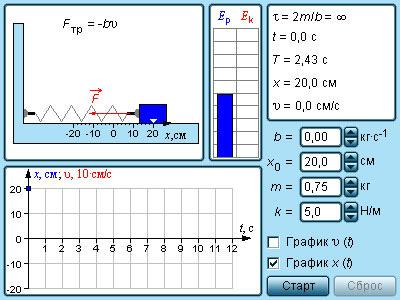
Рисунок Модель свободных колебаний груза на пружине.
Механические колебательные системы отличаются наличием сил упругих деформаций в каждой из них. Рисунок показывает угловой аналог гармонического осциллятора, совершающий крутильные колебания. Диск располагается горизонтально и висит на упругой нити, закрепленной в его центре масс. Если его повернуть на угол , тогда возникает момент силы упругой деформации кручения :
.
Данное выражение не соответствует закону Гука для деформации кручения. Величина аналогична жесткости пружины. Запись второго закона Ньютона для вращательного движения диска принимает вид
или , где моментом инерции обозначается , а – угловое ускорение.
Аналогично с формулой пружинного маятника:
.
Применение крутильного маятника замечено в механических часах. Он получил название балансира, в котором создание момента упругих сил производится при помощи спиралевидной пружины.
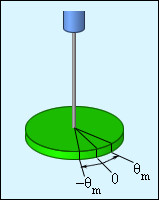
Рисунок Крутильный маятник.
Навигация по статьям
