Самоиндукция. Энергия магнитного поля

Содержание:

Преподаватель физики

Определение 1

Самоиндукция – это значимый частный случай электромагнитной индукции, когда магнитный поток, изменяясь и вызывая ЭДС индукции, создается током в самом контуре.

В случае, когда ток рассматриваемого контура по каким-либо причинам изменен, то имеет место изменение и магнитного поля этого тока, а значит и собственного магнитного потока, проходящего через контур. В контуре создается ЭДС самоиндукции, создавая препятствие для изменений тока в контуре (по правилу Ленца).

Собственный магнитный поток $Φ$ , который проходит через контур или катушку с током, является пропорциональным силе тока $I$ : $Φ = L I$ .

Определение 2

Коэффициент пропорциональности $L$ в формуле $Φ = L I$ есть коэффициент самоиндукции или индуктивность катушки. Единица индуктивности в $С И$ носит название генри $(Г н)$ . Индуктивность контура или катушки равна $1 Г н$ , когда при силе постоянного тока $1 А$ собственный поток составляет $1 В б$ : $1 Г н = \frac{1 В б}{1 А}$ .

Расчет индуктивности

Пример 1

Для наглядности произведем расчет индуктивности длинного соленоида, который имеет $N$ витков, площадь сечения $S$ и длину $l$ . Соленоид – это цилиндрическая катушка индуктивности, у которой длина много больше диаметра. Магнитное поле соленоида задается формулой:

$B = μ_{0} n I$ ,

где $I$ является обозначением тока в соленоиде, $n = \frac{N}{e}$ указывает число витков на единицу длины соленоида.

Магнитный поток внутри катушки соленоида, проходящий через все N витков, составляет:

$Φ = B \cdot S \cdot N = \frac{μ_{0} n^{2} S}{l}$

Таким образом, индуктивность соленоида будет выражена формулой:

$L = μ_{0} n^{2} S \cdot l = μ_{0} n^{2} V$ ,

где $V = S l$ – объем соленоида, содержащий магнитное поле.

Результат, который мы получили, не берет в расчет краевых эффектов, а значит он является приближенно верным лишь для катушек достаточной длины. Когда соленоид заполнен веществом, имеющим магнитную проницаемость $μ$ , при заданном токе $I$ индукция магнитного поля будет возрастать по модулю в $μ$ раз, а значит и индуктивность катушки с сердечником тоже получит увеличение в $μ$ раз:

$L_{μ} = μ \cdot L = μ_{0} \cdot μ \cdot n^{2} \cdot V$ .

Определение 3

ЭДС самоиндукции, которая возникает в катушке при постоянном значении индуктивности, в соответствии с законом Фарадея записывается в виде формулы:

$δ_{и н д} = δ_{L} = - \frac{∆ Φ}{∆ t} = - L \frac{∆ I}{∆ t}$ .

ЭДС самоиндукции является прямо пропорциональной индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле выступает носителем энергии. Так же, как заряженный конденсатор обладает запасом электрической энергии, катушка, по виткам которой проходит ток, обладает запасом магнитной энергии. Включив электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, при размыкании ключа будем наблюдать короткую вспышку лампы (рис. $1.21.1$ ). Ток в цепи появится под влиянием ЭДС самоиндукции. Источником энергии, которая будет выделяться в этом процессе электрической цепью, будет служить магнитное поле катушки.

Расчет индуктивности

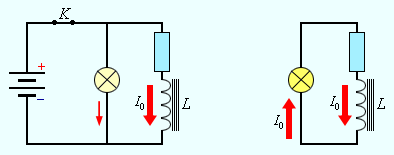
Рисунок $1.21.1 .$ Магнитная энергия катушки. В момент размыкания ключа $K$ лампа ярко вспыхнет.

Закон сохранения энергии позволяет говорить, что вся энергия, составляющая запас катушки, будет выделена в виде джоулева тепла. Обозначим как $R$ полное сопротивление цепи, тогда за время $Δ t$ будет выделено количество теплоты $Δ Q = I^{2} \cdot R \cdot Δ t$ .

Ток в цепи составляет:

$I = \frac{δ_{L}}{R} = - \frac{L}{R} \frac{∆ I}{∆ t}$

Выражение для $Δ Q$ можем записать так:

$∆ Q = - L \cdot I \cdot ∆ I = - Φ (I) ∆ I$

В данной записи $Δ I < 0$ ; значение тока в цепи постепенно снижается от изначального $I_{0}$ до нуля. Полное количество теплоты, которое выделится в цепи, возможно получить, осуществив действие интегрирования в пределах от $I_{0}$ до $0$ . Тогда получим:

$Q = \frac{L I_{0}^{2}}{2}$

Графический вывод формулы

Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока $Φ (I)$ от тока $I$ (рис. $1.21.2$ ). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. $1.21.2$ треугольника:

Графический вывод формулы

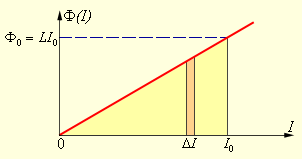
Рисунок $1.21.2 .$ Вычисление энергии магнитного поля.

В итоге формула энергии $W_{м}$ магнитного поля катушки с индуктивностью $L$ , создаваемого током $I$ , будет записана в виде формулы:

$W_{м} = \frac{Φ I}{2} = \frac{L I^{2}}{2} = \frac{Φ^{2}}{2 L}$

Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции $L_{μ}$ соленоида и для магнитного поля B, создаваемого током $I$ , получим запись:

$W_{м} = \frac{μ_{0} \cdot μ \cdot n^{2} \cdot I^{2}}{2} V = \frac{B^{2}}{2 μ_{0} \cdot μ} V$

В этой формуле $V$ является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.

Определение 4

Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: $W_{м} = \frac{B^{2}}{2 μ \cdot μ}$ .

В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.

Курсовая работа по физике

от 5 дней/ от 2160 р.

Реферат по физике

от 1 дня/ от 840 р.

Решение задач по физике

от 1 дня/ от 150 р.