
Статью подготовили специалисты образовательного сервиса Zaochnik.
Относительность промежутков времени
Содержание:
Выполнение физических измерений предусматривает пространственно-временные соотношения между событиями. В СТО их определяют в качестве физических явлений, происходящих в какой-либо точке пространства в определенный момент времени в выбранной системе отсчета.
Для полной характеристики события необходимо обратиться не только за выяснениями его физических свойств, но и знать его место и время. Для этого нужно применять процедуры измерения временных расстояний и промежутков. Это стало возможным после того, как Эйнштейн показал необходимость их строгого определения.
Синхронизация часов в СТО
Чтобы выбранная система отсчета выполняла точные измерения между двумя событиями, находящимися в одной точке пространства, необходимо иметь эталонные часы. Самыми точными считаются молекулярные и атомные часы. Они показывают четкие промежутки времени, так как их работа опирается на понятие одновременности.
Длительность какого-либо процесса определяется путем сравнения с интервалами времени, отделяющим показание часов, одновременное с концом процесса, от показания тех же часов, одновременного с началом процесса. Когда оба события происходят в разных точках системы отсчета, то для того, чтобы измерить промежутки времени между ними в этих точках, следует использовать синхронизированные часы.
Процедура синхронизации часов по Эйнштейну основана на независимости скорости света в пустоте от направления распространения.
Дано, что из точки с моментом времени при помощи часов посылается короткий световой импульс, как показано на рисунке Если время его прихода в и отражение назад на часах обозначить как , тогда отраженный сигнал возвращается в момент по часам . Из определения видно, что часы и работают синхронно при .
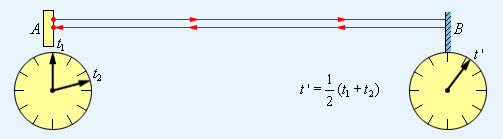
Рисунок Синхронизация часов в СТО.
Мировое время не зависит от системы отсчета, которая принимается как факт из классической физики. Оно эквивалентно неявному допущению о возможности синхронизации часов при помощи сигнала, распространяющегося с бесконечно большой скоростью.
Относительность промежутков времени
Расположение синхронизированных часов должно быть в разных точках выбранной системы.
События считаются одновременными, если синхронизированные часы показывают одинаковое время.
Имеется еще одна инерциальная система , движущаяся со скоростью в положительном направлении оси предложенной системы. Расположение часов и их синхронизация, описанная выше, выполняются в разных точках системы отсчета. Интервал времени теперь можно измерить как по часам из системы , так и по . Для определения эквивалентности промежутков необходимо обращаться к постулатам СТО.
Дано, что оба события системы происходят в одной и той же точке, а временной интервал между ними равняется по часам заданной системы. Он получил название собственного времени. Чтобы знать, существует ли промежуток времени между этими же событиями по измерению с помощью часов , нужно провести мысленный эксперимент.
Один конец твердого стержня с длиной имеет импульсную лампу , другой – отражающее зеркало . В системе стержень неподвижен и располагается параллельно относительно оси , как изображено на рисунке Событие характеризует вспышку лампы, а событие – вращение короткого светового импульса к лампе.
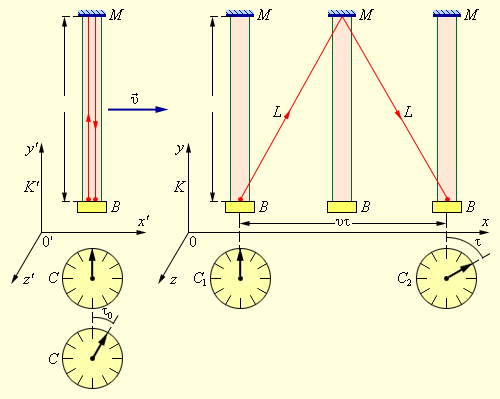
Рисунок Относительность промежутков времени. Моменты наступлений событий в системе фиксируются по одним и тем же часам , а в системе – по двум синхронизованным пространственно-разнесенным часам и . Система движется со скоростью в положительном направлении оси системы .
Система объясняет, что рассматриваемые события происходят в одной точке. Собственное время или промежуток времени между ними равняется . Если посмотреть со стороны наблюдателя, который находится в системе , то можно отметить движение светового импульса между зеркалами зигзагообразно с прохождением расстояния , равного , является интервалом времени между отправлением и возвращением светового импульса, который измерили с помощью синхронизированных часов и , располагаемых в разных точках системы . Исходя из второго постулата СТО, движение светового импульса в системе производится с той же скоростью, что и в системе . Отсюда следует .
Преобразуя соотношения, получаем связь между и :
, где .
Промежуток времени, который зависит от системы отсчета, является относительным. Значение собственного времени всегда меньше, чем интервал между заданными событиями, измеренными в другой системе отсчета. Данный эффект получил название релятивистского замедления времени.
Оно является следствием инвариантности скорости света.
Замедление времени считается взаимным, так как, основываясь на постулате о равноправии инерциальных систем и , для наблюдателя в или идут медленнее часы, которые связаны с системой, движущейся по отношению к наблюдателю. Такой вывод СТО нашел подтверждение при помощи опыта.
Во время исследования космических лучей обнаружили, что в их состав входят - мезоны - элементарные частицы с массой в раз больше массы электрона. Они нестабильны, время жизни равняется . Движение - мезонов в космических лучах достигает скорости света. Не учитывая релятивистский эффект замедления времени, их путь пролета в атмосфере равнялся бы . Из опыта известно, что они способны пролететь без распада большие расстояния. Исходя из СТО, средняя продолжительность жизни мезонов, согласно земным часам, равняется , потому как значение близко к .
Усредненный путь , который проходит мезон в земной системе отсчета, имеет более .
Парадокс близнецов
«Парадокс близнецов» связан с релятивистским эффектом замедления.
Суть парадокса близнецов:
Один из близнецов отправляется в космос с субсветовой скоростью. Так как, с точки зрения наблюдателя на Земле, время на космическом корабле идет медленнее, то по возвращению космонавт будет гораздо моложе оставшегося на Земле близнеца. Такое же заключение может сделать и другой брат, совершающий путешествие в космос. Для него оставшийся на Земле брат будет моложе после космического полета.
Для разрешения такого парадокса следует учитывать наличие неравноправных систем отсчета времени.
Тот, кто остается на Земле, находится в инерциальной системе отсчета, а тот, кто на корабле, – в принципиально инерциальной. При разгоне во время старта корабля с Земли он испытывает ускорение. Это же происходит во время изменения направления движения в дальней точке траектории или при торможении перед посадкой на Землю. Отсюда следует вывод, что вернувшийся брат-астронавт окажется моложе, исходя из СТО.
Эффекты замедления практически не уловимы при скорости корабля намного меньше, чем скорость света с. Ученые получили прямое подтверждение эффекта в экспериментах с макроскопическими часами.
Атомные часы работают с помощью пучков атомов цезия. Они способны тикать раз в секунду. При проведении сравнения их значения на Земле и на реактивном лайнере по предсказаниям СТО получили, что на лайнере происходило отставание на . Значение считалось ошибочным. Спустя время повтор эксперимента показал результат, удовлетворяющий СТО с точностью до .
На данный момент принимают во внимание релятивистский эффект замедления хода часов при переносе атомных на большие расстояния.
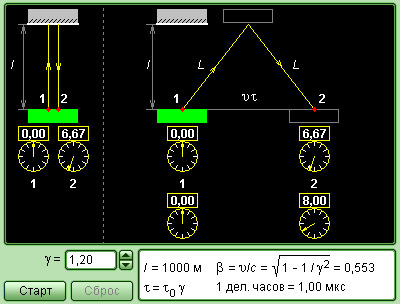
Рисунок Модель относительности промежутков времени.
Навигация по статьям
