
Статью подготовили специалисты образовательного сервиса Zaochnik.
Применение эвристических методов в обучении и педагогике
Содержание:
Термин «эвристика» происходит от греческого слова «эврика» — нашел, открыл (это высказывание приписывают Архимеду — его он выкрикнул, когда нашел решение заказанной ему задачи). Самоопределение эвристика формулируется (наиболее коротко и четко) как наука о том, как делать открытия».
Такое определение вывел Джордж Пойа (известный математик и педагог, автор книги «Математическое открытие»). Зародилась эвристика предположительно тогда, когда древнегреческими философами был сформулирован вопрос:
«Каким образом мы можем искать то, чего не знаем, а если мы знаем, что ищем, то зачем нам это искать?»
Что такое эвристика
В современном мире эвристика понимается как наука о продуктивном мышлении или наука о закономерностях организации процессов творческого/продуктивного мышления.
Из этого определения следует, что между эвристическими и творческими решениями имеется непосредственная связь. Если взять за основу то, что центром творчества является озарение («инсайт»), связанное с поиском оригинального решения проблемы, то эвристика — это наука об организации творческой деятельности, методах, приемах и правилах, лежащих в основе творческого процесса.
Подобная трактовка эвристики имеет непосредственную связь с сущностью педагогического процесса. Для того, чтобы понять каким образом и в соответствии с какими принципами организовывается творческий процесс решения задач, нужно взять за основу то, что это познание является набором рекомендаций, необходимых для построения творческого педагогического процесса. Такая обучающая процедура может именоваться эвристической педагогикой — педагогикой, основанной на принципах и правилах эвристики.
Прообразом эвристики многие считают майевтику. Такая аналогия была проведена на основании «сократических бесед» — бесед/споров, на протяжении которых Сократ (древнегреческий философ) приводил собеседника к правильному выводу посредством искусно подобранных вопросов, позволяя ему создавать новое (для собеседника) знание. Можно сказать, что Сократ выполнял функцию педагога, умело управляющего процессом познавательной деятельности обучаемого. При этом он не только управлял, но и показывал в момент бесед пример творческого решения задач.
Принципы эвристических решений
Рассмотреть принципы определения эвристического решения задачи можно на примере, описанном в книге Пойа (47а, 85-88). Там говорится о том, что Карл Фридрих Гаусс (ставший впоследствии «королем математиков»), будучи еще мальчиком решал задачу, заключающуюся в сложении ряда чисел от до . Эта довольно сложная задача была задана их учителем, который захотел немного отдохнуть. Но малыш Гаусс справился с ней гораздо раньше остальных учеников (практически сразу). При этом его решение оказалось единственным верным.
Автор книги обращает внимание на то, что мы не можем точно знать (и никогда не узнаем), как маленький Гаусс смог это сделать. Но если положиться на помощь воображения, можно предположить довольно правдоподобный ответ на этот вопрос. Гаусс скорее всего «видел» задачу глубоко и под нестандартным углом в отличие от других. Точнее — он смог увидеть, что каждая пара чисел, которые равноудалены от концов ряда , будучи сложенной вместе, дает неизменную сумму , поэтому общая сумма ряда будет равняться .
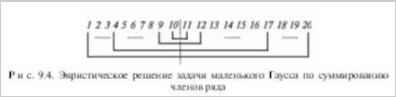
Этот пример наглядно показывает сущность эвристики и ее проблем. Для получения результатов есть множество путей, которые основываются на начальных условиях и знаниях, которыми обладает человек. Задача Гаусса помимо более длительного «лобового» пути, который как бы навязывается самой ситуацией, имеет множество других путей решения. При этот вариант, предложенный Гауссом, является не самым очевидным. Чтобы его реализовать необходимо сконцентрировать внимание сразу на двух концах ряда и увидеть симметрию его составляющих относительно середины и произвести попарное суммирование.
Если распределить все этапы решения в виде пути на графе потенциально возможных решений, то можно понять как много существует вариантов решения этой задачи.

На этой графе, которая представлена в виде лабиринта, имеется вход, расположенный в точке А и выход, размещенный в точке Б. Чтобы найти путь выхода из него необходимо перебрать множество вариантов. При этом и перебор, и время, затраченное на решение, могут резко сократиться при имении дополнительной информации: например, навыки в составлении карт и работы с компасом или знание того, куда нужно повернуть на развилке лабиринта.
Такие проблемы возникают при решении практически любой интеллектуальной задачи, будь то игра в шахматы, решение головоломки или планирование/решение творческих задач. Перебор всех имеющихся вариантов решения при неимении направляющих, принципиально важных идей или информации довольно быстро заканчивается «переборным взрывом».
Допустим, некто занят поиском шифра на кодовом замке сейфа. Если у этого человека нет абсолютно никакой информации, даже об общих принципах построения этого шифра, то он вряд ли сможет найти верное решение. Количество комбинаций будет лавинообразно увеличиваться при каждом повороте барабана.
Основываясь на подобном анализе большого количества прочих примеров можно определить понятие эвристического решения как решения, которое связано с резким уменьшением перебора вариантов возможных решений.
Рассмотрим в качестве примера шахматную игру. В набор самых элементарных эвристических рекомендаций входят следующие:
- контроль четырех центральных клеток поля;
- обеспечение безопасности короля;
- предотвращение вскрытия собственных вертикалей;
- защита фигур и многое другое.
Стоит отметить то, что все эти рекомендации не являются точными алгоритмами, это всего лишь направляющие действий шахматистов, которые способны существенно уменьшить количество потенциально верных решений. Если рассмотреть более тонкие шахматные эвристики, можно прийти к выводу, что они также не являются точными алгоритмами действий, которые способны привести к цели. Для эвристических правил характерна многозначность промежуточных результатов, поэтому категоричная точность рекомендаций не допускается (51:109-114). Эвристические рекомендации для шахмат представляют собой некие правила: например, наивысшее предпочтение отдается шаху, при помощи которого король противника отойдет от своей базы или хотя бы просто сдвинется.
Проанализировав подобные факты можно сделать вывод, что эвристичностью обладают суждения, являющиеся правдоподобными, которые повышают вероятность приближения к правильному решению. Такие рассуждения не точны, но их стратегия основывается в сужении всей области перебора до некоей зоны и направлении мышления на работу с узким классом понятий/фактов, базирующихся в ней. При этом нужно отметить, что эвристики не являются способом нахождения точных решений внутри этой зоны. Если охарактеризовать их по спортивной аналогии, то дело эвристик — это «закинуть шайбу в зону», но отнюдь не провести ее в ворота.
Примеры эвристических принципов
Законы эвристики являются скорее принципами, чем правилами, имеющими четкими границами условий применения. Возможно, более точно будет провести аналогию с понятием установки, которая имеет вид общего предписания к действию и считать эвристики мыслительными установками. Яркими примерами таких правил служат пословицы, афоризмы и поговорки. Например, «Сто раз отмерь, один раз отрежь», «Лучше синица в руке, чем журавль в небе», «Вода по каплям кувшин наполняет» и прочие — они указывают явное направление, но не дают точных предписаний к действию в конкретной ситуации.
В книге Пойа «Как решать задачу» (476: 99-103) приводится система английских пословиц, которая подбиралась автором в качестве иллюстраций основных этапов решения задач. Например, «Кто плохо понимает, тот плохо отвечает» — аналога этому нет в русском языке, но она очень точно формулирует классическое педагогическое высказывание «Прежде чем начинать решение задачи — пойми ее условия». Прочие пословицы, например, «Мудрый меняет свое решение, дурак — никогда», «Усердие — мать удачи», «Дуб валится с одного удара», «Где есть желание, найдется путь!» и им подобные содержат лишь общие рекомендации о направлении действий. Они побуждают к поиску личной заинтересованности в процессе/результате, проявлению настойчивости, продумыванию текущей ситуации с самых разных сторон.
Наиболее интересно рассмотрение правил поведения человека в обществе: в семье, коллективе, на производстве. Анализ известной книги Д. Карнеги «Как завоевывать друзей и оказывать влияние на людей» (27:84-93) ясно показывает, что почти все «правила Карнеги» являются эвристическими рекомендациями. Их смысл можно сформулировать как свод наставлений о том, какие правила следует использовать для достижения кратчайшего пути к завоеванию положения в обществе или достижения вершины карьеры, большого количества денег или любви окружающих. Чтобы наглядно доказать эвристичность и полезность этих рекомендаций, стоит привести их итоговую систему, которая называется «Девять способов изменить мнение людей, не вызывая при этом обиды или негодования (поведение руководителя на производстве):
- Беседу стоит начинать с искреннего восхищения и похвалы.
- Не стоит прямо говорить человеку о допущенных им ошибках.
- Перед критикой другого сначала указать на свои ошибки.
- Вместо раздачи приказаний нужно задавать вопросы.
- Всегда стоит давать возможность сохранить свою репутацию другому.
- Нужно хвалить других даже за малейшие достижения, при этом это нужно делать искренно и не скупясь на похвалы.
- Человеку нужно создать хорошую репутацию, которую он мог бы оправдать.
- Нужно прибегать к поощрениям, стараясь показать оппоненту, что ту ошибку, которую он совершил, легко исправить или то, что от него требуется легко осуществимо.
- Нужно поступать так, чтобы человек был счастлив выполнить предложенное.
Эвристические методы обучения или методы педагогической эвристики — это различные приемы/способы, которые использует педагог в процессе обучения умению находить творческие нестандартные решения как простых, так и нетривиальных задач.
Но чем же можно объяснить тот факт, что методы эвристики не дают возможности использовать точные правила, которые могут напрямую привести к решению задачи. Частично на это можно ответить на примере модели семантических сетей. Например, творческое решение задачи можно представить в виде перехода от одного узла знаний к другому. При этом переход, который проводится в трехмерной среде, служащей имитацией мозга или при помощи связи, которая имеет малый приоритет/редко используется, либо посредством построения новой связи. Тогда в пределах самой модели становится очевидным то, что является точной рекомендацией равнозначной решению. В обратном случае рекомендация способна только указывать направление решения, что делает ее эвристической.
Навигация по статьям
