Смешанное произведение векторов, его свойства, примеры и решения

Содержание:

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Для того, чтобы подробно рассмотреть такую тему, нужно охватить еще несколько разделов. Тема напрямую связана с такими терминами, как скалярное и векторное произведение. В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.

Термин

Для того, чтобы определить, в чем заключается данный термин, нужно взять три вектора.

Определение 1

Смешанным произведением $\vec{a}, \vec{b}$ и $\vec{d}$ является та величина, которая равняется скалярному произведению $[\vec{a} \times \vec{b}]$ и $\vec{d}$ , где $[\vec{a} \times \vec{b}]$ - умножение $\vec{a}$ и $\vec{b}$ . Операцию умножения $\vec{a}, \vec{b}$ и $\vec{d}$ зачастую обозначают $\vec{a} \cdot \vec{b} \cdot \vec{d}$ . Можно преобразовать формулу так: $\vec{a} \cdot \vec{b} \cdot \vec{d} = ([\vec{a} \times \vec{b}], \vec{d})$ .

Умножение в системе координат

Мы можем умножить вектора, если они указаны на координатной плоскости.

Возьмем $\vec{i}, \vec{j}, \vec{k}$

Произведение векторов в данном конкретном случае будет иметь следующий вид: $[\vec{a} \times \vec{b}] = (a_{y} \cdot b_{z} - a_{z} \cdot b_{y}) \cdot \vec{i} + (a_{z} \cdot b_{x} + a_{x} \cdot b_{z}) \cdot \vec{j} + (a_{x} \cdot b_{y} + a_{y} \cdot b_{x}) \cdot \vec{k} = |\begin{matrix} a_{y} & a_{z} \\ b_{y} & b_{z} \end{matrix}| \cdot \vec{i} - |\begin{matrix} a_{x} & a_{z} \\ b_{x} & b_{z} \end{matrix}| \cdot \vec{j} + |\begin{matrix} a_{x} & a_{y} \\ b_{x} & b_{y} \end{matrix}| \cdot \vec{k}$

Определение 2

Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.

Из этого следует:

$[\vec{a} \times \vec{b}] = (a_{y} \cdot b_{z} - a_{z} \cdot b_{y}) \cdot \vec{i} + (a_{z} \cdot b_{x} + a_{x} \cdot b_{z}) \cdot \vec{j} + (a_{x} \cdot b_{y} + a_{y} \cdot b_{x}) \cdot \vec{k} = |\begin{matrix} a_{y} & a_{z} \\ b_{y} & b_{z} \end{matrix}| \cdot \vec{i} - |\begin{matrix} a_{x} & a_{z} \\ b_{x} & b_{z} \end{matrix}| \cdot \vec{j} + |\begin{matrix} a_{x} & a_{y} \\ b_{x} & b_{y} \end{matrix}| \cdot \vec{k}$

Мы также можем определить смешанное произведение векторов, если в заданной системе координат указаны координаты векторов, которые умножаются.

$[\vec{a} \times \vec{b}] = (|\begin{matrix} a_{y} & a_{z} \\ b_{y} & b_{z} \end{matrix}| \cdot \vec{i} - |\begin{matrix} a_{x} & a_{z} \\ b_{x} & b_{z} \end{matrix}| \cdot \vec{j} + |\begin{matrix} a_{x} & a_{y} \\ b_{x} & b_{y} \end{matrix}| \cdot \vec{k}, d_{x} \cdot \vec{i} + d_{y} \cdot \vec{j} + d_{z} \cdot \vec{k}) = = |\begin{matrix} a_{y} & a_{z} \\ b_{y} & b_{z} \end{matrix}| \cdot d_{x} - |\begin{matrix} a_{x} & a_{z} \\ b_{x} & b_{z} \end{matrix}| \cdot d_{y} + |\begin{matrix} a_{x} & a_{y} \\ b_{x} & b_{y} \end{matrix}| \cdot d_{z} = |\begin{matrix} a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \\ d_{x} & d_{y} & d_{z} \end{matrix}|$

Таким образом, можно сделать вывод, что:

$\vec{a} \cdot \vec{b} \cdot d = (|\vec{a} \times \vec{b}|, \vec{d}) = |\begin{matrix} a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \\ d_{x} & d_{y} & d_{z} \end{matrix}|$

Определение 3

Смешанное произведение можно приравнять к определителю матрицы, в качестве строк которой использованы векторные координаты. Наглядно это выглядит так: $\vec{a} \cdot \vec{b} \cdot d = (|\vec{a} \times \vec{b}|, \vec{d}) = |\begin{matrix} a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \\ d_{x} & d_{y} & d_{z} \end{matrix}|$ .

Свойства операции над векторами Из особенностей, которые выделяются в скалярном или векторном произведении, можно вывести особенности, которые характеризуют смешанное произведение. Ниже мы приведем основные свойства.

$(λ \cdot \vec{a}) \cdot \vec{b} \cdot \vec{d} = \vec{a} \cdot (λ \cdot \vec{b}) \cdot \vec{d} = \vec{a} \cdot \vec{b} \cdot (λ \cdot \vec{d}) = λ \cdot \vec{a} \cdot \vec{b} \cdot \vec{d} λ \in R$ ;
$\vec{a} \cdot \vec{b} \cdot \vec{d} = \vec{d} \cdot \vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{d} \cdot \vec{a}; \vec{a} \cdot \vec{d} \cdot \vec{b} = \vec{b} \cdot \vec{a} \cdot \vec{d} = \vec{d} \cdot \vec{b} \cdot \vec{a}$ ;
$(\vec{a^{(1)}} + \vec{a^{(2)}}) \cdot \vec{b} \cdot \vec{d} = \vec{a^{(1)}} \cdot \vec{b} \cdot \vec{d} + \vec{a^{(2)}} \cdot \vec{b} \cdot \vec{d} \vec{a} \cdot (\vec{b^{(1)}} + \vec{b^{(2)}}) \cdot \vec{d} = \vec{a} \cdot \vec{b^{(1)}} \cdot \vec{d} + \vec{a} \cdot \vec{b^{(2)}} \cdot \vec{d} \vec{a} \cdot \vec{b} \cdot (\vec{d^{(1)}} + \vec{d^{(2)}}) = \vec{a} \cdot \vec{b} \cdot \vec{d^{(2)}} + \vec{a} \cdot \vec{b} \cdot \vec{d^{(2)}}$

Помимо приведенных свойств, следует уточнить, что если множитель нулевой, то результатом умножения также станет нуль.

Результатом умножения также будет нуль в том случае, если два или больше множителей равны.

Действительно, если $\vec{a} = \vec{b}$ , то, следуя определению векторного произведения $[\vec{a} \times \vec{b}] = |\vec{a}| \cdot \vec{|b|} \cdot \sin 0 = 0$ , следовательно, смешанное произведение равно нулю, так как $([\vec{a} \times \vec{b}], \vec{d}) = (\vec{0}, \vec{d}) = 0$ .

Если же $\vec{a} = \vec{b}$ или $\vec{b} = \vec{d}$ , то угол между векторами $[\vec{a} \times \vec{b}]$ и $\vec{d}$ равен $\frac{π}{2}$ . По определению скалярного произведения векторов $([\vec{a} \times \vec{b}], \vec{d}) = |[\vec{a} \times \vec{b}]| \cdot |\vec{d}| \cdot \cos \frac{π}{2} = 0$ .

Свойства операции умножения чаще всего требуются во время решения задач.
Для того, чтобы подробно разобрать данную тему, возьмем несколько примеров и подробно их распишем.

Пример 1

Докажите равенство $([\vec{a} \times \vec{b}], \vec{d} + λ \cdot \vec{a} + \vec{b}) = ([\vec{a} \times \vec{b}], \vec{d})$ , где $λ$ - некоторое действительное число.

Для того, чтобы найти решение этого равенства, следует преобразовать его левую часть. Для этого необходимо воспользоваться третьим свойством смешанного произведения, которое гласит:

$([\vec{a} \times \vec{b}], \vec{d} + λ \cdot \vec{a} + \vec{b}) = ([\vec{a} \times \vec{b}], \vec{d}) + ([\vec{a} \times \vec{b}], λ \cdot \vec{a}) + ([\vec{a} \times \vec{b}], \vec{b})$
Мы разобрали, что $(([\vec{a} \times \vec{b}], \vec{b}) = 0$ . Из этого следует, что
$([\vec{a} \times \vec{b}], \vec{d} + λ \cdot \vec{a} + \vec{b}) = ([\vec{a} \times \vec{b}], \vec{d}) + ([\vec{a} \times \vec{b}], λ \cdot \vec{a}) + ([\vec{a} \times \vec{b}], \vec{b}) = = ([\vec{a} \times \vec{b}], \vec{d}) + ([\vec{a} \times \vec{b}], λ \cdot \vec{a}) + 0 = ([\vec{a} \times \vec{b}], \vec{d}) + ([\vec{a} \times \vec{b}], λ \cdot \vec{a})$

Согласно первому свойству $([\overset{⇀}{a} \times \overset{⇀}{b}], λ \cdot \vec{a}) = λ \cdot ([\overset{⇀}{a} \times \overset{⇀}{b}], \vec{a})$ , а $([\overset{⇀}{a} \times \overset{⇀}{b}], \vec{a}) = 0$ . Таким образом, $([\overset{⇀}{a} \times \overset{⇀}{b}], λ \cdot \vec{a})$ . Поэтому,
$([\overset{⇀}{a} \times \overset{⇀}{b}], \vec{d} + λ \cdot \vec{a} + \vec{b}) = ([\overset{⇀}{a} \times \overset{⇀}{b}], \vec{d}) + ([\overset{⇀}{a} \times \overset{⇀}{b}], λ \cdot \vec{a}) = = ([\overset{⇀}{a} \times \overset{⇀}{b}], \vec{d}) + 0 = ([\overset{⇀}{a} \times \overset{⇀}{b}], \vec{d})$

Равенство доказано.

Пример 2

Необходимо доказать, что модуль смешанного произведения трех векторов не больше, чем произведения их длин.

Решение

Исходя из условия, можно представить пример в виде неравенства $|([\vec{a} \times \vec{b}], \vec{d})| \leq |\vec{a}| \cdot |\vec{b}| \cdot |\vec{d}|$ .

По определению, преобразуем неравенство $|([\vec{a} \times \vec{b}], \vec{d})| = |[\vec{a} \times \vec{b}]| \cdot |\vec{d}| \cdot |\cos ([\hat{\vec{a} \times \vec{b}}], \vec{d})| = = |\vec{a}| \cdot |\vec{b}| \cdot |\sin (\hat{\vec{a}, \vec{b}})| \cdot |\vec{d}| \cdot |\cos ([\hat{\vec{a} \times \vec{b}}], d)|$

Используя элементарные функции, можно сделать вывод, что $0 \leq |\sin (\hat{\vec{a}, \vec{b}})| \leq 1, 0 \leq |\cos ([\hat{\vec{a} \times \vec{b}}], \vec{d})| \leq 1$ .

Из этого можно сделать вывод, что
$|([\vec{a} \times \vec{b}], \vec{d})| = |\vec{a}| \cdot |\vec{b}| \cdot |\sin (\hat{\vec{a}, \vec{b})}| \cdot |\vec{d}| \cdot |\cos ([\hat{\vec{a} \times \vec{b}}], \vec{d})| \leq \leq |\vec{a}| \cdot |\vec{b}| \cdot 1 \cdot |\vec{d}| \cdot 1 = |\vec{a}| \cdot |\vec{b}| \cdot |\vec{d}|$

Неравенство доказано.

Разбор типовых задач

Для того, чтобы определить, чему равно произведение векторов, следует знать координаты умножаемых векторов. Для операции можно использовать такую формулу $\vec{a} \cdot \vec{b} \cdot \vec{d} = ([\vec{a} \times \vec{b}], \vec{d}) = |\begin{matrix} a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \\ d_{x} & d_{y} & d_{z} \end{matrix}|$ .

Пример 3

В прямоугольной системе координат представлены $3$ вектора с такими координатами: $\vec{a} = (1, - 2, 3), \vec{b} (- 2, 2, 1), \vec{d} = (3, - 2, 5)$ . Необходимо определить, чему равно произведение указанных векторов $\vec{a} \cdot \vec{b} \cdot \vec{d}$ .

Исходя из теории, представленной выше, мы можем воспользоваться правилом, которое гласит, что смешанное произведение может быть вычислено через определитель матрицы. Это будет выглядеть так: $\vec{a} \cdot \vec{b} \cdot \vec{d} = ([\vec{a} \times \vec{b}], \vec{d}) = |\begin{matrix} a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \\ d_{x} & d_{y} & d_{z} \end{matrix}| = |\begin{matrix} 1 & - 2 & 3 \\ - 2 & 2 & 1 \\ 3 & - 2 & 5 \end{matrix}| = = 1 \cdot 2 \cdot 5 + (- 1) \cdot 1 \cdot 3 + 3 \cdot (- 2) \cdot (- 2) - 3 \cdot 2 \cdot 3 - (- 1) \cdot (- 2) \cdot 5 - 1 \cdot 1 \cdot (- 2) = - 7$

Пример 4

Необходимо найти произведение векторов $\vec{i} + \vec{j}, \vec{i} + \vec{j} - \vec{k}, \vec{i} + \vec{j} + 2 \cdot \vec{k}$ , где $\vec{i}, \vec{j}, \vec{k}$ - орты прямоугольной декартовой системы координат.

Исходя из условия, которое гласит, что вектора расположены в данной системе координат, можно вывести их координаты: $\vec{i} + \vec{j} = (1, 1, 0) \vec{i} + \vec{j} - \vec{k} = (1, 1, - 1) \vec{i} + \vec{j} + 2 \cdot \vec{k} = (1, 1, 2)$

Используем формулу, которая использовалась выше
$([(\vec{i} + \vec{j}) \times (\vec{i} + \vec{j} - \vec{k}], (\vec{i} + \vec{j} + 2 \cdot \vec{k})) = |\begin{matrix} 1 & 1 & 0 \\ 1 & 1 & - 1 \\ 1 & 1 & 2 \end{matrix}| = 0 ([(\vec{i} + \vec{j}) \times (\vec{i} + \vec{j} - \vec{k}], (\vec{i} + \vec{j} + 2 \cdot \vec{k})) = 0$

Смешанное произведение также возможно определить с помощью длины вектора, которая уже известна, и угла между ними. Разберем этот тезис в примере.

Пример 5

В прямоугольной системе координат расположены три вектора $\vec{a}, \vec{b}$ и $\vec{d}$ , которые перпендикулярны между собой. Они представляют собой правую тройку, их длины составляют $4, 2$ и $3$ . Необходимо умножить вектора.

Обозначим $\vec{c} = [\vec{a} \times \vec{b}]$ .

Согласно правилу, результатом умножения скалярных векторов является число, которое равно результату умножения длин используемых векторов на косинус угла между ними. Делаем вывод, что $\vec{a} \cdot \vec{b} \cdot \vec{d} = ([\vec{a} \times \vec{b}], \vec{d}) = (\vec{c}, \vec{d}) = |\vec{c}| \cdot |\vec{d}| \cdot \cos (\hat{\vec{c}, \vec{d}})$ .

Используем длину вектора $\vec{d}$ , указанную в условии примера: $\vec{a} \cdot \vec{b} \cdot \vec{d} = |\vec{c}| \cdot |\vec{d}| \cdot \cos (\hat{\vec{c}, \vec{d}}) = 3 \cdot |\vec{c}| \cdot \cos (\hat{\vec{c}, \vec{d}})$ . Необходимо определить $|\vec{с}|$ и $\hat{(\vec{с}, \vec{d})}$ . По условию $(\hat{\vec{a}, \vec{b}}) = \frac{π}{2}, |\vec{a}| = 4, |\vec{b}| = 2$ . Вектор $\vec{c}$ найдем с помощью формулы: $|\vec{c}| = |[\vec{a} \times \vec{b}]| = |\vec{a}| \cdot |\vec{b}| \cdot \sin (\hat{\vec{a}, \vec{b}}) = 4 \cdot 2 \cdot \sin \frac{π}{2} = 8$
Можно сделать вывод, что $\vec{c}$ перпендикулярен $\vec{a}$ и $\vec{b}$ . Вектора $\vec{a}, \vec{b}, \vec{c}$ будут являться правой тройкой, так использована декартовая система координат. Векторы $\vec{c}$ и $\vec{d}$ будут однонаправленными, то есть, $(\hat{\vec{c}, \vec{d}}) = 0$ . Используя выведенные результаты, решаем пример $\vec{a} \cdot \vec{b} \cdot \vec{d} = 3 \cdot |\vec{c}| \cdot \cos (\hat{\vec{c}, \vec{d}}) = 3 \cdot 8 \cdot \cos 0 = 24$ .

$\vec{a} \cdot \vec{b} \cdot \vec{d} = 24$ .

Геометрический смысл

Используем множители $\vec{a}, \vec{b}$ и $\vec{d}$ .

Вектора $\vec{a}, \vec{b}$ и $\vec{d}$ исходят от одной точки. Используем их как стороны для построения фигуры.

Обозначим, что $\vec{c} = [\vec{a} \times \vec{b}]$ . Для данного случая можно определить произведение векторов как $\vec{a} \cdot \vec{b} \cdot \vec{d} = |\vec{c}| \cdot |\vec{d}| \cdot \cos (\hat{\vec{c}, \vec{d}}) = |\vec{c}| \cdot n p_{\vec{c}} \vec{d}$ , где $n p_{\vec{c}} \vec{d}$ - числовая проекция вектора $\vec{d}$ на направление вектора $\vec{c} = [\vec{a} \times \vec{b}]$ .

Абсолютная величина $n p_{\vec{c}} \vec{d}$ равняется числу, которое также является равно высоте фигуры, для которого использованы вектора $\vec{a}, \vec{b}$ и $\vec{d}$ в качестве сторон. Исходя из этого, следует уточнить, что $\vec{c} = [\vec{a} \times \vec{b}]$ перпендикулярен $\vec{a}$ и вектору и вектору согласно определению умножения векторов. Величина $\vec{c} = |[\vec{a} x \vec{b}]|$ равняется площади параллелепипеда, построенного на векторах $\vec{a}$ и $\vec{b}$ .

Делаем вывод, что модуль произведения $|\vec{a} \cdot \vec{b} \cdot \vec{d}| = |\vec{c}| \cdot |n p_{\vec{c}} \vec{d}|$ равен результату умножения площади основания на высоту фигуры, которая построена на векторах $\vec{a}, \vec{b}$ и $\vec{d}$ .

Определение 4

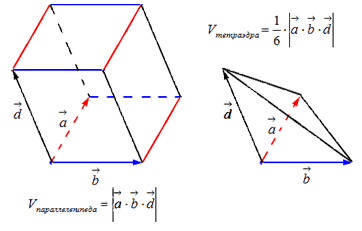
Абсолютная величина векторного произведения является объемом параллелепипеда: $V_{п а р а л л е л е п и п и д а} = |\vec{a} \cdot \vec{b} \cdot \vec{d}|$ .

Данная формула и является геометрическим смыслом.

Для того, чтобы закрепить знания, разберем несколько типичных примеров

Пример 6

Необходимо найти объем параллелепипеда, в качестве сторон которого используются $\vec{A B} = (3, 6, 3), \vec{A C} = (1, 3, - 2), \vec{A A_{1}} = (2, 2, 2)$ , заданные в прямоугольной системе координат. Объем параллелепипеда можно найти, используя формулу об абсолютной величине. Из этого следует: $\vec{A B} \cdot \vec{A C} \cdot \vec{A A_{1}} = |\begin{matrix} 3 & 6 & 3 \\ 1 & 3 & - 2 \\ 2 & 2 & 2 \end{matrix}| = 3 \cdot 3 \cdot 2 + 6 \cdot (- 2) \cdot 2 + 3 \cdot 1 \cdot 2 - 3 \cdot 3 \cdot 2 - 6 \cdot 1 \cdot 2 - 3 \cdot (- 2) \cdot 2 = - 18$

Тогда, $V_{п а р а л л е л е п и п е д а} = |- 18| = 18$ .

$V_{п а р а л л е л е п и п и д а} = 18$

Пример 7

В системе координат заданы точки $A (0, 1, 0), B (3, - 1, 5), C (1, 0, 3), D (- 2, 3, 1)$ . Следует определить объем тетраэдра, который расположен на этих точках.

Воспользуемся формулой $V_{т э т р а э д р а} = \frac{1}{6} \cdot |\vec{A B} \cdot \vec{A C} \cdot \vec{A D}|$ . Мы можем определить координаты векторов по координатам точек: $\vec{A B} = (3 - 0, - 1 - 1, 5 - 0) = (3, - 2, 5) \vec{A C} = (1 - 0, 0 - 1, 3 - 0) = (1, - 1, 3) \vec{A D} = (- 2 - 0, 3 - 1, 1 - 0) = (- 2, 2, 1)$

Дальше определяем смешанное произведение $\vec{A B} \cdot \vec{A C} \cdot \vec{A D}$ по координатам векторов: $\vec{A B} \cdot \vec{A C} \cdot \vec{A D} = |\begin{matrix} 3 & - 2 & 5 \\ 1 & - 1 & 3 \\ - 2 & 2 & 1 \end{matrix}| = 3 \cdot (- 1) \cdot 1 + (- 2) \cdot 3 \cdot (- 2) + 5 \cdot 1 \cdot 2 - 5 \cdot (- 1) \cdot (- 2) - (- 2) \cdot 1 \cdot 1 - 3 \cdot 3 \cdot 2 = - 7$ Объем $V_{т э т р а э д р а} = \frac{1}{6} \cdot |- 7| = \frac{7}{6}$ .

$V_{т э т р а э д р а} = \frac{7}{6}$ .

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.