Линейная зависимость системы векторов. Коллинеарные векторы

Содержание:

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

В данной статье мы расскажем:

что такое коллинеарные векторы;
какие существуют условия коллинеарности векторов;
какие существуют свойства коллинеарных векторов;
что такое линейная зависимость коллинеарных векторов.

Коллинеарные векторы

Определение 1

Коллинеарные векторы — это векторы, которые являются параллелями одной прямой или лежат на одной прямой.

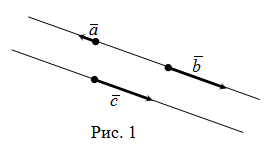
Условия коллинеарности векторов

Два векторы являются коллинеарными, если выполняется любое из следующих условий:

условие 1. Векторы $a$ и $b$ коллинеарны при наличии такого числа $λ$ , что $a = λ b$ ;
условие 2. Векторы $a$ и $b$ коллинеарны при равном отношении координат:

$a = (a_{1}; a_{2}), b = (b_{1}; b_{2}) \Rightarrow a ∥ b \Leftrightarrow \frac{a_{1}}{b_{1}} = \frac{a_{2}}{b_{2}}$

условие 3. Векторы $a$ и $b$ коллинеарны при условии равенства векторного произведения и нулевого вектора:

$a ∥ b \Leftrightarrow |a, b| = 0$

Замечание 1

Условие 2 неприменимо, если одна из координат вектора равна нулю.

Замечание 2

Условие 3 применимо только к тем векторам, которые заданы в пространстве.

Примеры задач на исследование коллинеарности векторов

Пример 1

Исследуем векторы $а = (1; 3)$ и $b = (2; 1)$ на коллинеарность.

Как решить?

В данном случае необходимо воспользоваться 2-м условием коллинеарности. Для заданных векторов оно выглядит так:

$\frac{1}{2} = \frac{- 3}{1}$

Равенство неверное. Отсюда можно сделать вывод, что векторы $a$ и $b$ неколлинеарны.

Ответ: $a | | b$

Пример 2

Какое значение $m$ вектора $a = (1; 2)$ и $b = (- 1; m)$ необходимо для коллинеарности векторов?

Как решить?

Используя второе условие коллинераности, векторы будут коллинеарными, если их координаты будут пропорциональными:

$\frac{1}{- 1} = \frac{2}{m}$

Отсюда видно, что $m = - 2 .$

Ответ: $m = - 2 .$

Критерии линейной зависимости и линейной независимости систем векторов

Теорема

Система векторов векторного пространства линейно зависима только в том случае, когда один из векторов системы можно выразить через остальные векторы данной системы.

Доказательство

Пусть система $\{e_{1}, e_{2}, . . ., e_{n}\}$ является линейно зависимой. Запишем линейную комбинацию этой системы равную нулевому вектору:

$a_{1} e_{1} + a_{2} e_{2} + . . . + a_{n} e_{n} = 0$

в которой хотя бы один из коэффициентов комбинации не равен нулю.

Пусть $a_{k} \neq 0 k \in \{1, 2, . . ., n\}$ .

Делим обе части равенства на ненулевой коэффициент:

${a_{k}}^{- 1} ({a_{k}}^{- 1} a_{1}) e_{1} + ({a_{k}}^{- 1} a_{k}) e_{k} + . . . + ({a_{k}}^{- 1} a_{n}) e_{n} = 0$

Обозначим:

$- {a_{k}}^{- 1} a_{m}$ , где $m \in \{1, 2, . . ., k - 1, k + 1, n\}$

В таком случае:

$β_{1} e_{1} + . . . + β_{k - 1} e_{k - 1} + β_{k + 1} e_{k + 1} + . . . + β_{n} e_{n} = 0$

или $e_{k} = (- β_{1}) e_{1} + . . . + (- β_{k - 1}) e_{k - 1} + (- β_{k + 1}) e_{k + 1} + . . . + (- β_{n}) e_{n}$

Отсюда следует, что один из векторов системы выражается через все остальные векторы системы. Что и требовалось доказать (ч.т.д.).

Достаточность

Пусть один из векторов можно линейно выразить через все остальные векторы системы:

$e_{k} = γ_{1} e_{1} + . . . + γ_{k - 1} e_{k - 1} + γ_{k + 1} e_{k + 1} + . . . + γ_{n} e_{n}$

Переносим вектор $e_{k}$ в правую часть этого равенства:

$0 = γ_{1} e_{1} + . . . + γ_{k - 1} e_{k - 1} - e_{k} + γ_{k + 1} e_{k + 1} + . . . + γ_{n} e_{n}$

Поскольку коэффициент вектора $e_{k}$ равен $- 1 \neq 0$ , у нас получается нетривиальное представление нуля системой векторов $\{e_{1}, e_{2}, . . ., e_{n}\}$ , а это, в свою очередь, означает, что данная система векторов линейно зависима. Что и требовалось доказать (ч.т.д.).

Следствие:

Система векторов является линейно независимой, когда ни один из ее векторов нельзя выразить через все остальные векторы системы.
Система векторов, которая содержит нулевой вектор или два равных вектора, линейно зависима.

Свойства линейно зависимых векторов

Для 2-х и 3-х мерных векторов выполняется условие: два линейно зависимых вектора — коллинеарны. Два коллинеарных вектора — линейно зависимы.
Для 3-х мерных векторов выполняется условие: три линейно зависимые вектора — компланарны. (3 компланарных вектора — линейно зависимы).
Для n-мерных векторов выполняется условие: $n + 1$ вектор всегда линейно зависимы.

Примеры решения задач на линейную зависимость или линейную независимость векторов

Пример 3

Проверим векторы $a = \{3, 4, 5\}$ , $b = \{- 3, 0, 5\}$ , $c = \{4, 4, 4\}$ , $d = \{3, 4, 0\}$ на линейную независимость.

Решение. Векторы являются линейно зависимыми, поскольку размерность векторов меньше количества векторов.

Пример 4

Проверим векторы $a = \{1, 1, 1\}$ , $b = \{1, 2, 0\}$ , $c = \{0, - 1, 1\}$ на линейную независимость.

Решение. Находим значения коэффициентов, при которых линейная комбинация будет равняться нулевому вектору:

$x_{1} a + x_{2} b + x_{3} c_{1} = 0$

Записываем векторное уравнение в виде линейного:

$\{\begin{cases} x_{1} + x_{2} = 0 \\ x_{1} + 2 x_{2} - x_{3} = 0 \\ x_{1} + x_{3} = 0 \end{cases}$

Решаем эту систему при помощи метода Гаусса:

$(\begin{matrix} 1 & 1 & 0 & | & 0 \\ 1 & 2 & - 1 & | & 0 \\ 1 & 0 & 1 & | & 0 \end{matrix}) ~$

Из 2-ой строки вычитаем 1-ю, из 3-ей — 1-ю:

$~ (\begin{matrix} 1 & 1 & 0 & | & 0 \\ 1 - 1 & 2 - 1 & - 1 - 0 & | & 0 - 0 \\ 1 - 1 & 0 - 1 & 1 - 0 & | & 0 - 0 \end{matrix}) ~ (\begin{matrix} 1 & 1 & 0 & | & 0 \\ 0 & 1 & - 1 & | & 0 \\ 0 & - 1 & 1 & | & 0 \end{matrix}) ~$

Из 1-й строки вычитаем 2-ю, к 3-ей прибавляем 2-ю:

$~ (\begin{matrix} 1 - 0 & 1 - 1 & 0 - (- 1) & | & 0 - 0 \\ 0 & 1 & - 1 & | & 0 \\ 0 + 0 & - 1 + 1 & 1 + (- 1) & | & 0 + 0 \end{matrix}) ~ (\begin{matrix} 0 & 1 & 0 & | & 1 \\ 0 & 1 & - 1 & | & 0 \\ 0 & 0 & 0 & | & 0 \end{matrix})$

Из решения следует, что у системы множество решений. Это значит, что существует ненулевая комбинация значения таких чисел $x_{1}, x_{2}, x_{3}$ , при которых линейная комбинация $a, b, c$ равняется нулевому вектору. Следовательно, векторы $a, b, c$ являются линейно зависимыми.

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.