
Статью подготовили специалисты образовательного сервиса Zaochnik.
Координаты вектора в декартовой системе координат (ДСК)
Содержание:
Для начала дадим определение координат вектора в заданной системе координат. Чтобы ввести данное понятие, определим что мы называем прямоугольной или декартовой системой координат.
Прямоугольная система координат представляет из себя прямолинейную систему координат с взаимно перпендикулярными осями на плоскости или в пространстве.
С помощью введения прямоугольной системы координат на плоскости или в трехмерном пространстве становится возможным описывание геометрических фигур вместе с их свойствами при помощи уравнений и неравенств, то есть использовать алгебраические методы при решении геометрических задач.
Тем самым, мы можем привязать к заданной системе координат векторы. Это значительно расширит наши возможности при решении определенных задач
Прямоугольная система координат на плоскости обычно обозначается , где и – оси коорднат. Ось называют осью абсцисс, а ось – осью ординат (в пространстве появляется ещё одна ось , которая перпендикулярна и и ).
Итак, нам дана прямоугольная декартова система координат на плоскости если мы отложим от начала координат векторы и , направление которых соответственно совпадет с положительными направлениями осей и , и их длина будет равна условной единице, мы получим координатные векторы. То есть в данном случае и являются координатными векторами.
Координатные векторы
Векторы и называются координатными векторами для заданной системы координат.
Откладываем от начала координат произвольный вектор . Опираясь на геометрическое определение операций над векторами, вектор может быть представлен в виде , где коэффициенты и - единственные в своем роде, их единственность достаточно просто доказать методом от противного.
Разложение вектора
Разложением вектора по координатным векторам и на плоскости называется представление вида .
Коэффициенты и называются координатами вектора в данной системе координат на плоскости.
Координаты вектора в данной системе координат принято записывать в круглых скобках, через запятую, при этом заданные координаты следует отделять от обозначения вектора знаком равенства. К примеру, запись означает, что вектор имеет координаты в данной системе координат и может быть представлен в виде разложения по координатным векторам и как.
Следует обратить внимание, что порядок записи координат, имеет важное значение, если вы запишите координаты вектора в другом порядке, вы получите совершенно другой вектор.
Опираясь на определения координат вектора и их разложения становится очевидным, что единичные векторы и имеют координаты и соответственно, и они могут быть представлены в виде следующих разложений .
Также имеет место быть нулевой вектор с координатами и разложением .
Равные и противоположные векторы
Векторыравны тогда, когда их соответствующие координаты равны.
Противоположным вектором называется вектор противоположный данному.
Отсюда следует, что координаты такого вектора будут противоположны координатам данного вектора, то есть, .
Все вышеизложенное можно аналогично определить и для прямоугольной системы координат, заданной в трехмерном пространстве. В такой системе координат имеет место быть тройка координатных векторов , а произвольный вектор раскладывается не по двум, а уже по трем координатам, причем единственным образом и имеет вид , а коэффициенты этого разложения называются координатами вектора в данной (трехмерной) системе координат.
Следовательно, координатные векторы в трехмерном пространстве принимают также значение 1 и имеют координаты , , , координаты нулевого вектора также равны нулю , и в таком случае два вектора будут считаться равными, если все три соответствующие координаты векторов между собой равны , и координаты противоположного вектора противоположны соответствующим координатам вектора , то есть, .
Координаты радиус-вектора точки
Чтобы ввести данное определение, требуется показать в данной системе координат связь координат точки и координат вектора.
Пусть нам дана некоторая прямоугольная декартова система координат и на ней задана произвольная точка с координатами .
Вектор называется радиус-вектором точки .
Определим, какие координаты в данной системе координат имеет радиус-вектор точки
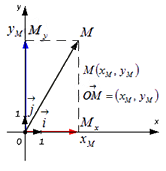
Вектор имеет вид суммы , где точки и это проекции точки М на координатные прямые Ox и Oy соответственно (данные рассуждения следуют из определения проекция точки на прямую), а и - координатные векторы, следовательно, вектор имеет координаты в данной системе координат.
Иначе говоря, координаты радиус-вектора точки М равны соответствующим координатам точки М в прямоугольной декартовой системе координат.
Аналогично в трехмерном пространстве радиус-вектор точки разлагается по координатным векторам как , следовательно, .
Навигация по статьям
