Деление отрезка в заданном соотношении: координаты точки

Содержание:

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Когда существуют условия деления отрезка в определенном отношении, необходимо уметь определять координаты точки, служащей разделителем. Выведем формулу для нахождения этих координат, поставив задачу на плоскости.

Определение координат точки, делящей отрезок в заданном отношении, на плоскости

Исходные данные: задана прямоугольная система координат $O x y$ и две лежащие на ней, несовпадающие точки с заданными координатами $A (x_{A}, y_{A})$ и $B (x_{B}, y_{B})$ . А также задана точка $С$ , делящая отрезок $А В$ в отношении $λ$ (некоторое положительное действительное число). Необходимо определить координаты точки $С$ : $x_{C}$ и $y_{C}$ .

Перед тем, как приступить к решению поставленной задачи, немного раскроем смысл заданного условия: «точка $С$ , делящая отрезок $А В$ в отношении $λ$ ». Во-первых, это выражение свидетельствует о том, что точка $С$ лежит на отрезке $А В$ (т.е. между точками $А$ и $В$ ). Во-вторых, понятно, что согласно заданному условию отношение длин отрезков $А С$ и $С В$ равно $λ$ . Т.е. верно равенство:

$\frac{|A C|}{|C B|} = λ$ .

В этом случае точка $А$ – начало отрезка, точка $В$ – конец отрезка. Если бы было задано, что точка $С$ делит в заданном отношении отрезок $В А$ , тогда верным было бы равенство: .

Ну и совсем очевидный факт, что если $λ = 1$ , то точка $С$ является серединой отрезка $А В$ .

Решим поставленную задачу при помощи векторов. Отобразим произвольно в некой прямоугольной системе координат точки $А$ , $В$ и точку $С$ на отрезке $А В$ . Построим радиус-векторы указанных точек, а также векторы $\vec{A C}$ и $\vec{C B}$ . Согласно условиям задачи, точка $С$ делит отрезок $А В$ в отношении $λ$ .

Определение координат точки, делящей отрезок в заданном отношении, на плоскости

Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: $\vec{O A} = (x_{A}, y_{A})$ и $\vec{O B} = (x_{B}, y_{B})$ .

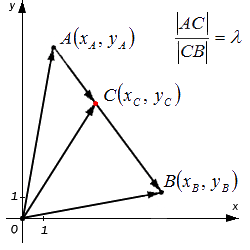
Определим координаты вектора : они будут равны координатам точки $С$ , которые и требуется найти по условию задачи.

Используя операцию сложения векторов, запишем равенства: $\vec{O C} = \vec{O A} + \vec{A C} \vec{O B} = \vec{O C} + \vec{C B} \Leftrightarrow \vec{C B} = \vec{O B} - \vec{O C}$

По условию задачи точка $С$ делит отрезок $А В$ в отношении $λ$ , т.е. верно равенство $|A C| = λ \cdot |C B|$ .

Векторы $\vec{A C}$ и $\vec{C B}$ лежат на одной прямой и являются сонаправленными. $λ > 0$ по условию задачи, тогда, согласно операции умножения вектора на число, получим: $\vec{A C} = λ \cdot \vec{C B}$ .

Преобразуем выражение, подставив в него : $\vec{C B} = \vec{O B} - \vec{O C}$ .

$\vec{A C} = λ \cdot (\vec{O B} - \vec{O C})$ .

Равенство $\vec{O C} = \vec{O A} + \vec{A C}$ перепишем как $\vec{O C} = \vec{O A} + λ \cdot (\vec{O B} - \vec{O C})$ .

Используя свойства операций над векторами, из последнего равенства следует: $\vec{O C} = \frac{1}{1 + λ} \cdot (\vec{O A} + λ \cdot \vec{O B})$ .

Теперь нам остается непосредственно вычислить координаты вектора $\vec{O C} = \frac{1}{1 + λ} \cdot (\vec{O A} + λ \cdot \vec{O B})$ .

Выполним необходимые действия над векторами $\vec{O A}$ и $\vec{O B}$ .

$\vec{O A} = (x_{A}, y_{A})$ и $\vec{O B} = (x_{B}, y_{B})$ , тогда $\vec{O A} + λ \cdot \vec{O B} = (x_{A} + λ \cdot x_{B}, y_{A} + λ \cdot y_{B})$ .

Таким образом, $\vec{O C} = \frac{1}{1 + λ} \cdot (\vec{O A} + λ \cdot \vec{O B}) = (\frac{x_{A} + λ \cdot x_{B}}{1 + λ}, \frac{y_{A} + λ \cdot y_{B}}{1 + λ})$ .

Резюмируя: координаты точки $С$ , делящей отрезок $А В$ в заданном отношении $λ$ определяются по формулам : $x_{C} = \frac{x_{A} + λ \cdot x_{B}}{1 + λ}$ и $y_{C} = \frac{у_{A} + λ \cdot y_{B}}{1 + λ}$ .

Определение координат точки, делящей отрезок в заданном отношении, в пространстве

Исходные данные: прямоугольная система координат $O x y z$ , точки с заданными координатами $A (x_{A}, y_{A}, z_{A})$ и $B (x_{B}, y_{B}, z_{B})$ .

Точка $С$ делит отрезок $А В$ в отношении $λ$ . Необходимо определить координаты точки $С$ .

Используем ту же схему рассуждений, что и в случае выше на плоскости, придем к равенству:

$\vec{O C} = \frac{1}{1 + λ} \cdot (\vec{O A} + λ \cdot \vec{O B})$

Векторы и являются радиус-векторами точек $А$ и $В$ , а значит:

$\vec{O A} = (x_{A}, y_{A}, z_{A})$ и $\vec{O B} = (x_{B}, y_{B}, z_{B})$ , следовательно

$\vec{O C} = \frac{1}{1 + λ} \cdot (\vec{O A} + λ \cdot \vec{O B}) = (\frac{x_{A} + λ \cdot x_{B}}{1 + λ}, \frac{y_{A} + λ \cdot y_{B}}{1 + λ}, \frac{z_{A} + λ \cdot z_{B}}{1 + λ})$

Таким образом, точка $С$ , делящая отрезок $А В$ в пространстве в заданном отношении $λ$ , имеет координаты: $(\frac{x_{A} + λ \cdot x_{B}}{1 + λ}, \frac{y_{A} + λ \cdot y_{B}}{1 + λ}, \frac{z_{A} + λ \cdot z_{B}}{1 + λ})$

Рассмотрим теорию на конкретных примерах.

Пример 1

Исходные данные: точка $С$ делит отрезок $А В$ в отношении пять к трем. Координаты точек $А$ и $В$ заданы $A (11, 1, 0), B (- 9, 2, - 4)$ .

Решение

По условию задачи $λ = \frac{5}{3}$ . Применим полученные выше формулы и получим:

$\frac{x_{A} + λ \cdot x_{B}}{1 + λ} = \frac{11 + \frac{5}{3} \cdot (- 9)}{1 + \frac{5}{3}} = - \frac{3}{2}$

$\frac{y_{A} + λ \cdot y_{B}}{1 + λ} = \frac{1 + \frac{5}{3} \cdot 2}{1 + \frac{5}{3}} = \frac{13}{8}$

$\frac{z_{A} + λ \cdot z_{B}}{1 + λ} = \frac{0 + \frac{5}{3} \cdot (- 4)}{1 + \frac{5}{3}} = - \frac{5}{2}$

Ответ: $C (- \frac{3}{2}, \frac{13}{8}, - \frac{5}{2})$

Пример 2

Исходные данные: необходимо определить координаты центра тяжести треугольника $А В С$ .

Заданы координаты его вершин: $A (2, 3, 1), B (4, 1, - 2), C (- 5, - 4, 8)$

Решение

Известно, что центром тяжести любого треугольника является точка пересечения его медиан (пусть это будет точка $М$ ). Каждая из медиан делится точкой $М$ в отношении $2$ к $1$ , считая от вершины. Исходя из этого, найдем ответ на поставленный вопрос.

Допустим, что $А D$ – медиана треугольника $А В С$ . Точка $М$ – точка пересечения медиан, имеет координаты $M (x_{M}, y_{M}, z_{M})$ и является центром тяжести треугольника. $М$ , как точка пересечения медиан, делит отрезок $А D$ в отношении $2$ к $1$ , т.е. $λ = 2$ .

Найдем координаты точки $D$ . Так как $A D$ – медиана, то точка $D$ – середина отрезка $В С$ . Тогда, используя формулу нахождения координат середины отрезка, получим:

$x_{D} = \frac{x_{B} + x_{C}}{2} = \frac{4 + (- 5)}{2} = - \frac{1}{2} y_{D} = \frac{y_{B} + y_{C}}{2} = \frac{1 + (- 4)}{2} = - \frac{3}{2} z_{D} = \frac{z_{B} + z_{C}}{2} = \frac{- 2 + 8}{2} = 3$

Вычислим координаты точки $М$ :

$x_{M} = \frac{x_{A} + λ \cdot x_{D}}{1 + λ} = \frac{2 + 2 \cdot (- \frac{1}{2})}{1 + 2} = \frac{1}{3}$

$y_{M} = \frac{y_{A} + λ \cdot y_{D}}{1 + λ} = \frac{3 + 2 \cdot (- \frac{3}{2})}{1 + 2} = 0$

$z_{M} = \frac{z_{A} + λ \cdot z_{D}}{1 + λ} = \frac{1 + 2 \cdot 3}{1 + 2} = \frac{7}{3}$

Ответ: $(\frac{1}{3}, 0, \frac{7}{3})$

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.