
Статью подготовили специалисты образовательного сервиса Zaochnik.
Основные тригонометрические тождества, их формулировки и вывод
Содержание:
В этой статье мы разберем такие важные понятия в тригонометрии, как арксинус, арккосинус, арктангенс и арккотангенс. Мы можем найти значения чисел (углов), если знаем данные тригонометрических функций; это и есть та самая задача, что приводит нас к обратным функциям.
Ниже мы не только дадим определения основных понятий и общепринятые обозначения, но и приведем расчеты, из которых будет ясно, что они из себя представляют. В конце мы попробуем связать понятия арккотангенса, арктангенса, арккосинуса и арксинуса с понятием единичной окружности.
Основные определения
Все перечисленные выше понятия - арксинус, арккосинус, арктангенс и арккотангенс – можно рассматривать как в качестве числа, так и в качестве угла. Ранее мы уже говорили о такой же двойственности восприятия прямых функций (синус, косинус и др.) Рассмотрим оба подхода отдельно.
Арксинус и другие обратные функции как угол
Допустим, у нас есть некий угол, синус которого равен . Обозначим его буквой альфа.
Итак, . Такое значение синуса может быть у бесконечного числа углов: , где . Поэтому нам потребуется ввести дополнительные условия. Пусть угол альфа будет не менее и не более градусов (т.е. (в радианах он будет принадлежать отрезку ),). В таком случае наше равенство позволит обозначить угол альфа более ясно: в таких условиях им будет только один угол – в градусов ( радианов).
Исходя из указанного равенства, мы можем сделать вывод, что угол альфа определяется при условии любого числа и условии . Этот угол - и есть арксинус числа .
Сформулируем основные определения.
- Арксинус - это функция, обратная . Для некоторого числа а она представляет собой угол от до градусов, которого равен .
- Арккосинус - функция, обратная косинусу. Для числа - это такой угол, которого равен , и который при этом находится в диапазоне от до градусов.
- Арктангенс -тригонометрическая функция, обратная тангенсу. Для некоторого числа u это угол, величина которого находится в диапазоне от до градусов, тангенс которого равен .
- Арккотангенс числа а есть также угол величиной от до градусов, котангенс которого равен .
Подытожим: так, запись означает всего лишь угол, синус которого равняется ; - угол с косинусом и так далее.
Подписи вида и являются общепринятыми для записи обратных тригонометрических функций. Иногда в справочниках, особенно тех, что составлены на английском языке, можно встретить немного другие обозначения для арккотангенса и арктангенса - и . Они значат то же самое, но у нас не распространены, поэтому пользоваться ими мы не будем.
Вышеуказанные определения можно сформулировать в более краткой и символической форме:
- arcsin числа а в диапазоне от минус единицы до единицы есть угол с величиной ()
- arccos числа а в диапазоне от минус единицы до единицы есть угол с величиной ()
- arctg любого числа а есть угол с величиной ()
- arctg любого числа а есть угол с величиной что
Обратите внимание, что в определениях arcsin и arccos стоит диапазон от минус единицы до плюс единицы, а для двух других функций а может быть любым числом. Получается, что арксинус - ошибочная запись, ведь тройка не принадлежит у указанному диапазону. Также бессмысленны записи , , и с любыми другими значениями, которые выходят за пределы нужного нам отрезка, ведь синус и косинус не бывают больше единицы и меньше минус единицы. В случае с арктангенсом и арккотангенсом такой проблемы нет, для них подойдет любое действительное число, в том числе ноль, пи и так далее.
Теперь разберем примеры обратных функций числа. Для начала возьмем арксинус. Из его базового определения следует, что угол - арксинус числа , таким образом, (в данном случае и ).
- число, которое меньше единицы и больше минус единицы, а угол находится в пределах от до и .
Другими примерами являются записи вида , , . При этом не может быть , потому что .
Возьмем следующий пример: градусов - минус единица, но при этом обратное неверно: угол - не арксинус , потому что должен быть не более градусов. Угол в градусов не является арксинусом ни одного числа, потому что лежит за пределами нужного диапазона.
Найдем примеры других обратных функций. Так, угол радианов есть арккосинус , т.е, .Здесь все условия арккосинуса выполняются, число принадлежит нужному отрезку, угол заданной величины находится в пределах от нуля до пи и . Угол - арккосинус нуля: .
Согласно определению арктангенса, значения или . Арктангенс корня из трех равен градусам ( рад) . Из этого можно сделать вывод, что , так как угол лежит в рамках от до и .
Если вы хотите более подробно изучить такой подход к определению обратных тригонометрических функций, рекомендуем вам учебник Кочеткова (ч.1, стр. 260-278)
Арксинус и другие обратные функции как число
В том случае, если в задаче речь идет, скажем, о синусе угла, то логично его арксинус также воспринимать как угол. Если нам нужно, например, вычислить косинус некоторого числа, то тут важно встать на другую точку зрения и рассмотреть обратные функции как числа. Исходя из второго подхода, можно немного переформулировать определения:
- Арксинус а есть некоторое число, , синус которого равен .
- Арккосинус числа есть некоторое число , косинус которого равен .
- Арктангенс числа - это такое число , тангенс которого равен .
- Арккотангенс числа есть такое число , котангенс которого равен .
Такие формулировки типичны для большинства современных учебников по математике.
Небольшой пример: арксинус числа - это , таким образом, (здесь и .
Какой же подход следует выбирать? Как понять, когда лучше рассматривать значения арксинуса и прочих функций как углы, а когда - как числа? Это можно понять из контекста задачи. Обычно если там упоминается, скажем, , то это угол. Если мы видим запись вида , то, скорее всего, это просто число или же угол, измеренный в радианах. Если же встречаются просто формулировки вида и др. без указаний чисел и значений, то мы вольны выбирать любой подход, который хотим.
Объяснение обратных функций с позиции геометрии
Более наглядно представить обратные функции числа можно геометрически: ведь если это углы, их можно изобразить на чертеже. Это просто сделать, если вы еще не забыли базовые определения основных прямых функций.
Для этого нам понадобится уже знакомая нам единичная окружность. Ее дуги, связывающие между собой основные углы, и будут соответствовать величинам обратных функций.
Например, возьмем дугу, которая проиллюстрирует нам арксинус некого числа . Проведем линию синусов и укажем на ней точку в соответствии с величиной . Из этой точки теперь нужно попасть к оси абсцисс (возьмем положительное направление). У нас получился луч, который пересечет окружность в особой точке. Арксинус числа - это и есть часть дуги окружности от этой точки до начала координат. Вспомним два подхода к рассмотрению функций: как угол и как число. Угол, соответствующий дуге, - это иллюстрация арксинуса в рамках первого подхода, а длина дуги, выраженная количественно, иллюстрирует арксинус в рамках второго.
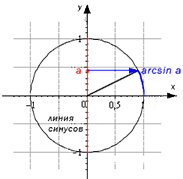
Теперь нарисуем дуги, которые проиллюстрируют для нас остальные обратные функции. На втором графике они отмечены синими линиями. Взгляните, как можно графически отобразить понятия для произвольного числа (в указанных выше диапазонах):
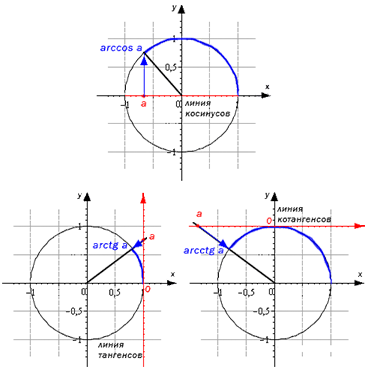
Вывод: что такое аркфункции
В итоге мы можем сформулировать следующее: для любого числа можно вычислить углы - арксинус и арккосинус, а для каждого действительного числа - углы арктангенс и арккотангенс. Эта точка зрения позволяет сопоставить между собой числовое значение аргумента и конкретный угол, который является значением функции.
Мы можем смотреть на понятия и как на числа и как на углы. Если мы берем их в качестве чисел, то они являются числовыми функциями: каждому значению а соответствует число.
Подытожим: все эти четыре понятия - и есть обратные тригонометрические функции. Название понятно: арксинус противопоставлен синусу, арккосинус - косинусу, арктангенс - тангенсу, арккотангенс - котангенсу. Поэтому еще одно распространенное собирательное название для них - аркфункции.
Навигация по статьям
