
Статью подготовили специалисты образовательного сервиса Zaochnik.
Уравнение плоскости, виды уравнения плоскости
Содержание:
В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат трехмерного пространства.
Определение уравнения плоскости
Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.
Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными и . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.
Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.
Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.
Общее уравнение плоскости
Сформулируем теорему, а затем запишем уравнение плоскости.
Всякая плоскость в прямоугольной системе координат в трехмерном пространстве может быть задана уравнением вида , где и – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид , определяет плоскость в трехмерном пространстве
Уравнение, имеющее вид носит название общего уравнения плоскости. Если не придавать числам и конкретных значений, то мы получаем уравнение плоскости в общем виде.
Важно понимать, что уравнение , будет точно так же определять плоскость. В уравнении - это некоторое отличное от нуля действительное число. Это значит, что равенства и равнозначны.
Общим уравнениям плоскости и удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.
Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида .
Уравнение плоскости может быть полным и неполным. Все коэффициенты и в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.
Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.
Рассмотрим положение в пространстве плоскости, заданной уравнением .
Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости . Уравнение определяет координатную плоскость , а общее уравнение плоскости вида соответствует плоскости, которая проходит через начало координат.
Важное уточнение: коэффициенты и в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.
Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.
Нормальное уравнение плоскости
Нормальное уравнение плоскости – это общее уравнение плоскости вида , которое удовлетворяет следующим условиям: длина вектора равна единице, т.е. , а .
Также запись нормального уравнения плоскости может иметь следующий вид , где – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а - это направляющие косинусы нормального вектора данной плоскости единичной длины.
То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат удалена от начала координат на расстояние в положительном направлении нормального вектора этой плоскости . Если равно нулю, то плоскость проходит через начало координат.
Плоскость задана общим уравнением плоскости вида . , нормальный вектор этой плоскости имеет длину, равную единице, так как . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.
Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.
Уравнение плоскости в отрезках
Плоскость отсекает на координатных осях и отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами и . Уравнение плоскости в отрезках имеет вид . Знак чисел и показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.
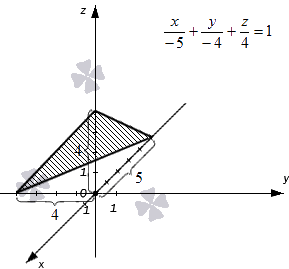
Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках .
Точки удалены от начала координат в отрицательном направлении на единиц по оси абсцисс, на единицы в отрицательном направлении по оси ординат и на единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.
Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид .
Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.
Навигация по статьям
