Расстояние между скрещивающимися прямыми: определение и примеры нахождения

Содержание:

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Статья нацелена на нахождение расстояния между скрещивающимися прямыми методом координат. Будет рассмотрено определение расстояния между этими прямыми, получим алгоритм при помощи которого преобразуем нахождение расстояния между скрещивающимися прямыми. Закрепим тему решением подобных примеров.

Расстояние между скрещивающимися прямыми – определение

Предварительно необходимо доказать теорему, которая определяет связь между заданными скрещивающимися прямыми.

Раздел взаимного расположения прямых в пространстве говорит о том, что если две прямые называют скрещивающимися, если их расположение не в одной плоскости.

Теорема

Через каждую пару скрещивающихся прямых может проходить плоскость, параллельная данной, причем только одна.

Расстояние между скрещивающимися прямыми – определение — Доказательство

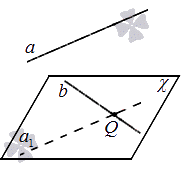
При переходе от определения расстояния между скрещивающимися прямыми определяем расстояние через расстояние между прямой и параллельной ей плоскостью.

Определение 1

Расстоянием между скрещивающимися прямыми называют расстояние между одной из скрещивающихся прямых и параллельной ей плоскостью, проходящей через другую прямую.

То есть расстояние между прямой и плоскостью является расстоянием от заданной точки к плоскости. Тогда применима формулировка определения расстояния между скрещивающимися прямыми.

Определение 2

Расстоянием между скрещивающимися прямыми называют расстояние от некоторой точки скрещивающихся прямых к плоскости, проходящей через другую прямую, параллельную первой прямой.

Произведем подробное рассмотрение прямых $a$ и $b$ . Точка $М_{1}$ располагается на прямой $a$ , через прямую $b$ проводится плоскость $χ$ , параллельная прямой $a$ . Из точки $М_{1}$ проводим перпендикуляр $М_{1} Н_{1}$ к плоскости $χ$ . Длина этого перпендикуляра является расстоянием между скрещивающимися прямыми $a$ и $b$ . Рассмотрим на рисунке, приведенном ниже.

Расстояние между скрещивающимися прямыми – определение

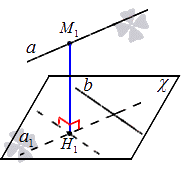
Нахождение расстояния между скрещивающимися прямыми – теория, примеры, решения

Расстояния между скрещивающимися прямыми находятся при построении отрезка. Искомое расстояние равняется длине этого отрезка. По условию задачи его длина находится по теореме Пифагора, по признакам равенства или подобия треугольников или другим.

Когда имеем трехмерное пространство с системой координат $О х у z$ с заданными в ней прямыми $a$ и $b$ , то вычисления следует проводить, начиная с расстояния между заданными скрещивающимися при помощи метода координат. Произведем подробное рассмотрение.

Пусть по условию $χ$ является плоскостью, проходящей через прямую $b$ , которая параллельна прямой $a$ . Искомое расстояние между скрещивающимися прямыми $a$ и $b$ равняется расстоянию от точки $М_{1}$ , расположенной на прямой $a$ , к плоскости _ $χ$ . Для того, чтобы получить нормальное уравнение плоскости $χ$ , необходимо определить координаты точки $M_{1} (x_{1}, y_{1}, z_{1})$ _,расположенной на прямой $a$ . Тогда получим $\cos α \cdot x + \cos β \cdot y + \cos γ \cdot z - p = 0$ , которое необходимо для определения расстояния $|M_{1} H_{1}|$ от точки $M_{1} (x_{1}, y_{1}, z_{1})$ к плоскости $χ$ . Вычисления производятся по формуле $|M_{1} H_{1}| = |\cos α \cdot x_{1} + \cos β \cdot y_{1} + \cos γ \cdot z_{1} - p|$ . Необходимое расстояние равняется искомому расстоянию между скрещивающимися прямыми.

Данная задача предполагает получение координат точки $М_{1}$ , которая располагается на прямой $a$ , нахождение нормального уравнения плоскости $χ$ .

Определение координат точки $М_{1}$ необходимо и возможно при знании основных видов уравнений прямой в пространстве. Чтобы получить уравнение плоскости $χ$ , необходимо остановиться подробней на алгоритме вычисления.

Если координаты $(x_{2}, y_{2}, z_{2})$ будут определены при помощи точки $М_{2}$ , через которую проведена плоскость $χ$ , получаем нормальный вектор плоскости $χ$ в виде вектора $\vec{n} = (A, B, C)$ . Следуя из этого, можно записать общее уравнение плоскости $χ$ в виде $A \cdot (x - x_{2}) + B \cdot (y - y_{2}) + C \cdot (z - z_{2}) = 0$ .

Вместо точки $М_{2}$ может быть взята любая другая точка, принадлежащая прямой $b$ , потому как плоскость $χ$ проходит через нее. Значит, координаты точки $М_{2}$ найдены. Необходимо перейти к нахождению нормального вектора плоскости $χ$ .

Имеем, что плоскость $χ$ проходит через прямую $b$ , причем параллельна прямой $a$ . Значит, нормальный вектор плоскости $χ$ перпендикулярен направляющему вектору прямой $a$ , обозначим $\vec{a}$ , и направляющему вектору прямой $b$ , обозначим $\vec{b}$ . Вектор $\vec{n}$ будет равняться векторному произведению $\vec{a}$ и $\vec{b}$ , что значит, $\vec{n} = [\vec{a} \times \vec{b}]$ . После определения координат $(a_{x}, a_{y}, a_{z})$ и $(b_{x}, b_{y}, b_{z})$ направляющих векторов заданных прямых $a$ и $b$ , вычисляем

$\vec{n} = [\vec{a} \times \vec{b}] = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \end{matrix}|$

Отсюда находим значение координат $(A, B, C)$ нормального вектора к плоскости $χ$ .

Знаем, что общее уравнение плоскости $χ$ имеет вид $A \cdot (x - x_{2}) + B \cdot (y - y_{2}) + C \cdot (z - z_{2}) = 0$ .

Необходимо привести уравнение к нормальному виду $\cos α \cdot x + \cos β \cdot y + \cos γ \cdot z - p = 0$ . После чего нужно произвести вычисления искомого расстояния между скрещивающимися прямыми $a$ и $b$ , исходя из формулы $|M_{1} H_{1}| = |\cos α \cdot x_{1} + \cos β \cdot y_{1} + \cos γ \cdot z_{1} - p|$ .

Чтобы найти расстояние между скрещивающимися прямыми $a$ и $b$ , необходимо следовать алгоритму:

определение координат $(x_{1}, y_{1}, z_{1})$ и $(x_{2}, y_{2}, z_{2})$ точек $М_{1}$ и $М_{2}$ , расположенных на прямых $a$ и $b$ соответственно;
получение координат $(a_{x}, a_{y}, a_{z})$ и $(b_{x}, b_{y}, b_{z})$ , принадлежащих направляющим векторам прямых $a$ и $b$ ;
нахождение координат $(A, B, C)$ , принадлежащих вектору $\vec{n}$ на плоскости $χ$ , проходящей через прямую $b$ , расположенную параллельно $a$ , по равенству $\vec{n} = [\vec{a} \times \vec{b}] = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \end{matrix}|$ ;
запись общего уравнения плоскости $χ$ в виде $A \cdot (x - x_{2}) + B \cdot (y - y_{2}) + C \cdot (z - z_{2}) = 0$ ;
приведение полученного уравнения плоскости $χ$ к уравнению нормального вида $\cos α \cdot x + \cos β \cdot y + \cos γ \cdot z - p = 0$ ;
вычисление расстояния $|M_{1} H_{1}|$ от $M_{1} (x_{1}, y_{1}, z_{1})$ к плоскости $χ$ , исходя из формулы $|M_{1} H_{1}| = |\cos α \cdot x_{1} + \cos β \cdot y_{1} + \cos γ \cdot z_{1} - p|$ .

Пример 1

Имеются две скрещивающиеся прямые в прямоугольной системе координат $О х у z$ трехмерного пространства. Прямая $a$ определена параметрическим уравнением прямой в пространстве $\{\begin{cases} \begin{array}{l} x = - 2 \\ y = 1 + 2 \cdot λ \end{array} \\ z = 4 - 3 \cdot λ \end{cases}$ , прямая $b$ при помощи канонического уравнения прямой в пространстве $\frac{x}{1} = \frac{y - 1}{- 2} = \frac{z + 4}{6}$ . Найти расстояние между скрещивающимися прямыми.

Решение

Понятно, что прямая а пересекает точку $M_{1} (- 2, 1, 4)$ с направляющим вектором $\vec{a} = (0, 2, - 3)$ , а прямая $b$ пересекает точку $M_{2} (0, 1, - 4)$ с направляющим вектором $\vec{b} = (1, - 2, 6)$ .

Для начала следует произвести вычисление направляющих векторов $\vec{a} = (0, 2, - 3)$ и $\vec{b} = (1, - 2, 6)$ по формуле. Тогда получаем, что

$[\vec{a} \times \vec{b}] = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ 0 & 2 & - 3 \\ 1 & - 2 & 6 \end{matrix}| = 6 \cdot \vec{i} - 3 \cdot \vec{j} - 2 \cdot \vec{k}$

Отсюда получаем, что $\vec{n} = [\vec{a} \times \vec{b}]$ - это вектор плоскости $χ$ , который проходит через прямую $b$ параллельно $a$ с координатами $(6, - 3, - 2)$ . Получим:

$6 \cdot (x - 0) - 3 \cdot (y - 1) - 2 \cdot (z - (- 4)) = 0 \Leftrightarrow 6 x - 3 y - 2 z - 5 = 0$

Находим нормирующий множитель для общего уравнения плоскости $6 x - 3 y - 2 z - 5 = 0$ . Вычислим по формуле $\frac{1}{\sqrt{6^{2} + {(- 3)}^{2} + {(- 2)}^{2}}} = \frac{1}{7}$ . Значит, нормальное уравнение примет вид $\frac{6}{7} x - \frac{3}{7} y - \frac{2}{7} z - \frac{5}{7} = 0$ .

Необходимо воспользоваться формулой, чтобы найти расстояние от точки $M_{1} (- 2, 1, 4)$ до плоскости, заданной уравнением $\frac{6}{7} x - \frac{3}{7} y - \frac{2}{7} z - \frac{5}{7} = 0$ . Получаем, что

$|M_{1} H_{1}| = |\frac{6}{7} \cdot (- 2) - \frac{3}{7} \cdot 1 - \frac{2}{7} \cdot 4 - \frac{5}{7}| = |\frac{- 28}{7}| = 4$

Отсюда следует, что искомым расстоянием является расстояние между заданными скрещивающимися прямыми, является значение $4$ .

Ответ: $4$ .

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.