
Статью подготовили специалисты образовательного сервиса Zaochnik.
Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости
Содержание:
Статья рассматривает понятия параллельность прямой и плоскости. Будут рассмотрены основные определения и приведены примеры. Рассмотрим признак параллельности прямой к плоскости с необходимыми и достаточными условиями параллельности, подробно решим примеры заданий.
Параллельные прямые и плоскость – основные сведения
Прямая и плоскость называются параллельными, если не имеют общих точек, то есть не пересекаются.
Параллельность обозначается «». Если в задании по условию прямая и плоскость параллельны, тогда обозначение имеет вид . Рассмотрим рисунок, приведенный ниже.
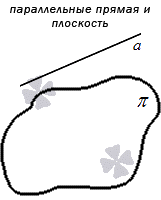
Считается, что прямая , параллельная плоскости и плоскость , параллельная прямой , равнозначные, то есть прямая и плоскость параллельны друг другу в любом случае.
Параллельность прямой и плоскости – признак и условия параллельности
Не всегда очевидно, что прямая и плоскость параллельны. Зачастую это нужно доказать. Необходимо использовать достаточное условие, которое даст гарантию на параллельность. Такой признак имеет название признака параллельности прямой и плоскости. Предварительно рекомендуется изучить определение параллельных прямых.
Если заданная прямая , не лежащая в плоскости , параллельна прямой , которая принадлежит плоскости , тогда прямая параллельна плоскости .
Рассмотрим теорему, используемую для установки параллельности прямой с плоскостью.
Если одна из двух параллельных прямых параллельна плоскости, то другая прямая лежит в этой плоскости либо параллельна ей.
Подробное доказательство рассмотрено в учебнике класса по геометрии. Необходимым и достаточным условием параллельности прямой с плоскостью возможно при наличии определения направляющего вектора прямой и нормального вектора плоскости.
Для параллельности прямой , не принадлежащей плоскости , и данной плоскости необходимым и достаточным условием является перпендикулярность направляющего вектора прямой с нормальным вектором заданной плоскости.
Условие применимо, когда необходимо доказать параллельность в прямоугольной системе координат трехмерного пространства. Рассмотрим подробное доказательство.
Допустим, прямая а в систему координат задается каноническими уравнениями прямой в пространстве , которые имеют вид или параметрическими уравнениями прямой в пространстве , плоскостью с общими уравнениями плоскости .
Отсюда является направляющим вектором с координатами прямой а, - нормальным вектором заданной плоскости альфа.
Чтобы доказать перпендикулярность и , нужно использовать понятие скалярного произведения. То есть при произведении результат должен быть равен нулю из условия перпендикулярности векторов.
Значит, что необходимым и достаточным условием параллельности прямой и плоскости запишется так . Отсюда является направляющим вектором прямой с координатами, а - нормальным вектором плоскости .
Определить, параллельны ли прямая с плоскостью .
Решение
Получаем, что предоставленная прямая не принадлежит плоскости, так как координаты прямой не подходят. При подстановке получаем, что .
Необходимо проверить на выполнимость необходимое и достаточное условие параллельности прямой и плоскости. Получим, что координаты направляющего вектора прямой имеют значения .
Нормальным вектором для плоскости считается . Перейдем к вычислению скалярного произведения векторов и . Получим, что .
Значит, перпендикулярность векторов и очевидна. Отсюда следует, что прямая с плоскостью являются параллельными.
Ответ: прямая с плоскостью параллельны.
Определить параллельность прямой в координатной плоскости , когда даны координаты .
Решение
По условию видно, что точка не лежит на оси , так как значение не равно .
Для плоскости вектор с координатами считается нормальным вектором данной плоскости. Обозначим направляющий вектор прямой как . Теперь при помощи координат начала и конца рассчитаем координаты вектора . Получим, что . Необходимо выполнить проверку на выполнимость необходимого и достаточного условия векторов и , чтобы определить их перпендикулярность.
Запишем .
Отсюда следует, что прямая с координатной плоскостью не являются параллельными.
Ответ: не параллельны.
Не всегда заданное условие способствует легкому определению доказательства параллельности прямой и плоскости. Появляется необходимость в проверке принадлежности прямой плоскости . Существует еще одно достаточное условие, при помощи которого доказывается параллельность.
При заданной прямой с помощью уравнения двух пересекающихся плоскостей , плоскостью - общим уравнением плоскости .
Необходимым и достаточным условием для параллельности прямой и плоскости яляется отсутствие решений системы линейных уравнений, имеющей вид .
Из определения следует, что прямая с плоскостью не должна иметь общих точек, то есть не пересекаться, только в этом случае они будут считаться параллельными. Значит, система координат не должна иметь точек, принадлежащих ей и удовлетворяющих всем уравнениям:
, а также уравнению плоскости .
Следовательно, система уравнений, имеющая вид , называется несовместной.
Верно обратное: при отсутствии решений системы не существует точек в , удовлетворяющих всем заданным уравнениям одновременно. Получаем, что нет такой точки с координатами, которая могла бы сразу быть решениями всех уравнений и уравнения . Значит, имеем параллельность прямой и плоскости, так как отсутствуют их точки пересечения.
Система уравнений не имеет решения, когда ранг основной матрицы меньше ранга расширенной. Это проверяется теоремой Кронекера-Капелли для решения линейных уравнений. Можно применять метод Гаусса для определения ее несовместимости.
Доказать , что прямая параллельна плоскости .
Решение
Для решения данного примера следует переходить от канонического уравнения прямой к виду уравнения двух пересекающихся плоскостей. Запишем это так:
Чтобы доказать параллельность заданной прямой с плоскостью , необходимо уравнения преобразовать в систему уравнений .
Видим, что она не решаема, значит прибегнем к методу Гаусса.
Расписав уравнения, получаем, что .
Отсюда делаем вывод, что система уравнений является несовместной, так как прямая и плоскость не пересекаются, то есть не имеют общих точек.
Делаем вывод, что прямая и плоскость параллельны, так как было выполнено необходимое и достаточное условие для параллельности плоскости с заданной прямой.
Ответ: прямая и плоскость параллельны.
Навигация по статьям
