
Статью подготовили специалисты образовательного сервиса Zaochnik.
Вычисление площади фигуры, ограниченной параметрически заданной кривой
Содержание:
Когда мы выясняли геометрический смысл определенного интеграла, у нас получилась формула, с помощью которой можно найти площадь криволинейной трапеции, ограниченной осью абсцисс, прямыми , а также непрерывной (неотрицательной или неположительной) функцией . Иногда удобнее задавать функцию, ограничивающую фигуру, в параметрическом виде, т.е. выражать функциональную зависимость через параметр . В рамках данного материала мы покажем, как можно найти площадь фигуры, если она ограничена параметрически заданной кривой.
После объяснения теории и выведения формулы мы разберем несколько характерных примеров на нахождение площади таких фигур.
Основная формула для вычисления
Допустим, что у нас имеется криволинейная трапеция, границами которой являются прямые , ось и параметрически заданная кривая , а функции и являются непрерывными на интервале будет непрерывно возрастать на нем и .
Чтобы вычислить площадь трапеции при таких условиях, нужно использовать формулу .
Мы вывели ее из формулы площади криволинейной трапеции методом подстановки :
Учитывая монотонное убывание функции на интервале , нужная формула принимает вид .
Если функция не относится к основным элементарным, то нам понадобится вспомнить основные правила возрастания и убывания функции на интервале, чтобы определить, будет ли она возрастающей или убывающей.
Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой
В этом пункте мы разберем несколько задач на применение формулы, выведенной выше.
Условие: найдите площадь фигуры, которую образует линия, заданная уравнениями вида .
Решение
У нас есть параметрически заданная линия. Графически ее можно отобразить в виде эллипса с двумя полуосями и . См на иллюстрацию:

Попробуем найти площадь полученной фигуры, которая занимает первый квадрант. Область находится в интервале . Далее умножим полученное значение на и найдем площадь целой фигуры.
Вот ход наших вычислений:
При , равном , мы получим интервал . Функция на нем будет монотонно убывать (подробнее см. статью об основных элементарных функциях и их свойствах). Значит, можно применить формулу вычисления площади и найти определенный интеграл, используя формулу Ньютона-Лейбница:
Значит, площадь фигуры, заданной исходной кривой, будет равна .
Ответ:
Уточним, что при решении задачи выше можно было взять не только четверть эллипса, но и его половину – верхнюю или нижнюю. Одна половина будет расположена на интервале . В этом случае у нас бы получилось:
Таким образом, при равном , мы получили . Функция на этом интервале будет монотонно убывать.
После этого вычисляем площадь половины эллипса:
Важно отметить, что можно взять только верхнюю или нижнюю часть, а правую или левую нельзя.
Можно составить параметрическое уравнение данного эллипса, центр которого будет расположен в начале координат. Оно будет иметь вид . Действуя так же, как и в примере выше, получим формулу для вычисления площади эллипса .
Задать окружность, центр которой расположен в начале координат, можно с помощью уравнения , где является параметром, а – радиусом данной окружности. Если мы сразу воспользуемся формулой площади эллипса, то то у нас получится формула, с помощью которой можно вычислить площадь круга с радиусом : .
Разберем еще одну задачу.
Условие: найдите, чему будет равна площадь фигуры, которая ограничена параметрически заданной кривой .
Решение
Сразу уточним, что данная кривая имеет вид вытянутой астроиды. Обычно астроида выражается с помощью уравнения вида .
Теперь разберем подробно, как построить такую кривую. Выполним построение по отдельным точкам. Это самый распространенный метод, который применим для большинства задач. Более сложные примеры требуют проведения дифференциального исчисления, чтобы выявить параметрически заданную функцию.
У нас .
Данные функции являются определенными для всех действительных значений . Для и известно, что они являются периодическими и их период составляет пи. Вычислив значения функций для некоторых , получим точки .
Составим таблицу итоговых значений:
После этого отметим нужные точки на плоскости и соединим их одной линией.
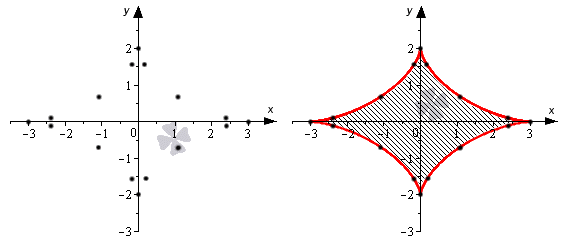
Теперь нам надо найти площадь той части фигуры, что находится в первой координатной четверти. Для нее :
Если равен , то у нас получится интервал , и функция на нем будет монотонно убывать. Теперь берем формулу площади и считаем:
У нас получились определенные интегралы, которые можно вычислить с помощью формулы Ньютона-Лейбница. Первообразные для этой формулы можно найти, используя рекуррентную формулу , где .
Мы вычислили площадь четверти фигуры. Она равна .
Если мы умножим это значение на , получим площадь всей фигуры – .
Точно таким же образом мы можем доказать, что площадь астроиды, заданной уравнениями , можно найти по формуле , а площадь фигуры, которая ограничена линией , считается по формуле .
Навигация по статьям
