
Статью подготовили специалисты образовательного сервиса Zaochnik.
Нахождение площади фигуры, ограниченной линиями y=f(x), x=g(y)
Содержание:
В предыдущем разделе, посвященном разбору геометрического смысла определенного интеграла, мы получили ряд формул для вычисления площади криволинейной трапеции:
для непрерывной и неотрицательной функции на отрезке ,
для непрерывной и неположительной функции на отрезке .
Эти формулы применимы для решения относительно простых задач. На деле же нам чаще придется работать с более сложными фигурами. В связи с этим, данный раздел мы посвятим разбору алгоритмов вычисления площади фигур, которые ограничены функциями в явном виде, т.е. как или .
Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
Пусть функции и определены и непрерывны на отрезке , причем для любого значения из . Тогда формула для вычисления площади фигуры , ограниченной линиями и будет иметь вид .
Похожая формула будет применима для площади фигуры, ограниченной линиями и : .
Разберем три случая, для которых формула будет справедлива.
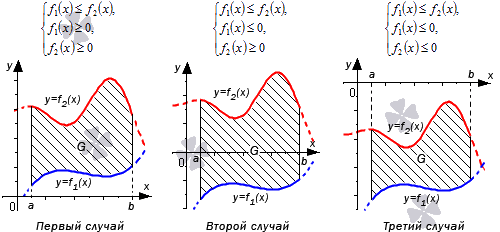
В первом случае, учитывая свойство аддитивности площади, сумма площадей исходной фигуры и криволинейной трапеции равна площади фигуры . Это значит, что
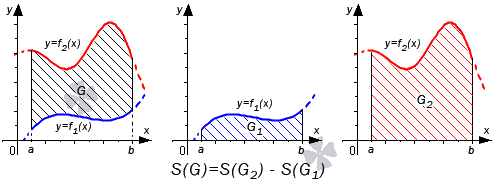
Поэтому, .
Выполнить последний переход мы можем с использованием третьего свойства определенного интеграла.
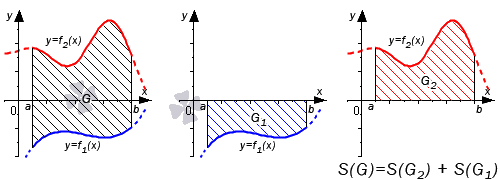
Во втором случае справедливо равенство:
Графическая иллюстрация будет иметь вид:
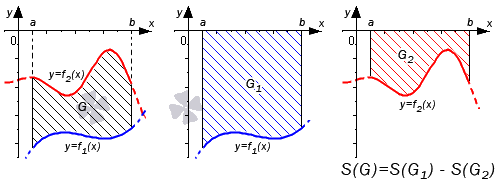
Если обе функции неположительные, получаем: . Графическая иллюстрация будет иметь вид:
Перейдем к рассмотрению общего случая, когда и пересекают ось .
Точки пересечения мы обозначим как . Эти точки разбивают отрезок на частей , где . Фигуру можно представить объединением фигур . Очевидно, что на своем интервале попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как
Следовательно,
Последний переход мы можем осуществить с использованием пятого свойства определенного интеграла.
Проиллюстрируем на графике общий случай.
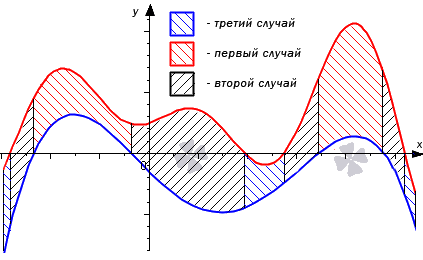
Формулу можно считать доказанной.
А теперь перейдем к разбору примеров вычисления площади фигур, которые ограничены линиями и .
Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
Рассмотрение любого из примеров мы будем начинать с построения графика. Изображение позволит нам представлять сложные фигуры как объединения более простых фигур. Если построение графиков и фигур на них вызывает у вас затруднения, можете изучить раздел об основных элементарных функциях, геометрическом преобразовании графиков функций, а также построению графиков во время исследования функции.
Необходимо определить площадь фигуры, которая ограничена параболой и прямыми линиями , .
Решение
Изобразим линии на графике в декартовой системе координат.
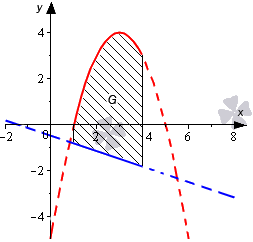
На отрезке график параболы расположен выше прямой . В связи с этим, для получения ответа используем формулу, полученную ранее, а также способ вычисления определенного интеграла по формуле Ньютона-Лейбница:
Ответ:
Рассмотрим более сложный пример.
Необходимо вычислить площадь фигуры, которая ограничена линиями .
Решение
В данном случае мы имеем только одну прямую линию, расположенную параллельно оси абсцисс. Это . Это требует от нас найти второй предел интегрирования самостоятельно.
Построим график и нанесем на него линии, данные в условии задачи.
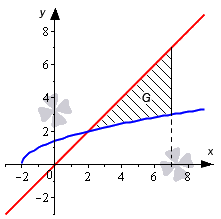
Имея график перед глазами, мы легко можем определить, что нижним пределом интегрирования будет абсцисса точки пересечения графика прямой и полу параболы . Для нахождения абсциссы используем равенства:
Получается, что абсциссой точки пересечения является .
Обращаем ваше внимание на тот факт, что в общем примере на чертеже линии пересекаются в точке , поэтому такие подробные вычисления могут показаться излишними. Мы привели здесь такое подробное решение только потому, что в более сложных случаях решение может быть не таким очевидным. Это значит, что координаты пересечения линий лучше всегда вычислять аналитически.
На интервале график функции расположен выше графика функции . Применим формулу для вычисления площади:
Ответ:
Необходимо вычислить площадь фигуры, которая ограничена графиками функций и .
Решение
Нанесем линии на график.
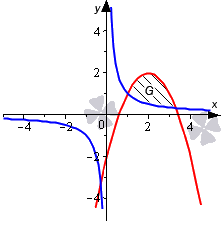
Определимся с пределами интегрирования. Для этого определим координаты точек пересечения линий, приравняв выражения и . При условии, что не равно нулю, равенство становится эквивалентным уравнению третьей степени с целыми коэффициентами. Освежить в памяти алгоритм по решению таких уравнений мы можете, обратившись к разделу «Решение кубических уравнений».
Корнем этого уравнения является : .
Разделив выражение на двучлен , получаем:
Оставшиеся корни мы можем найти из уравнения :
Мы нашли интервал , на котором фигура заключена выше синей и ниже красной линии. Это помогает нам определить площадь фигуры:
Ответ:
Необходимо вычислить площадь фигуры, которая ограничена кривыми и осью абсцисс.
Решение
Нанесем все линии на график. Мы можем получить график функции из графика , если расположим его симметрично относительно оси абсцисс и поднимем на одну единицу вверх. Уравнение оси абсцисс .
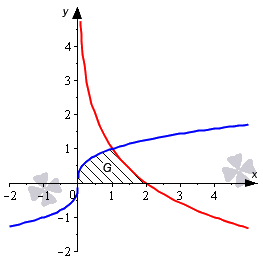
Обозначим точки пересечения линий.
Как видно из рисунка, графики функций и пересекаются в точке . Так получается потому, что является единственным действительным корнем уравнения .
является единственным корнем уравнения , поэтому графики функций и пересекаются в точке .
является единственным корнем уравнения . В связи с этим графики функций и пересекаются в точке . Последнее утверждение может быть неочевидным, но уравнение не может иметь более одного корня, так как функция является строго возрастающей, а функция строго убывающей.
Дальнейшее решение предполагает несколько вариантов.
Вариант №1
Фигуру мы можем представить как сумму двух криволинейных трапеций, расположенных выше оси абсцисс, первая из которых располагается ниже средней линии на отрезке , а вторая ниже красной линии на отрезке . Это значит, что площадь будет равна .
Вариант №2
Фигуру можно представить как разность двух фигур, первая из которых расположена выше оси абсцисс и ниже синей линии на отрезке , а вторая между красной и синей линиями на отрезке . Это позволяет нам найти площадь следующим образом:
В этом случае для нахождения площади придется использовать формулу вида . Фактически, линии, которые ограничивают фигуру, можно представить в виде функций от аргумента .
Разрешим уравнения и относительно :
Получим искомую площадь:
Ответ:
Необходимо вычислить площадь фигуры, которая ограничена линиями .
Решение
Красной линией нанесем на график линию, заданную функцией . Синим цветом нанесем линию , черным цветом обозначим линию .
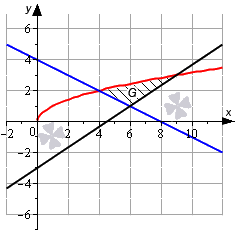
Отметим точки пересечения.
Найдем точки пересечения графиков функций и :
Найдем точку пересечения графиков функций и :
Найдем точку пересечения линий и :
Дальше мы можем продолжить вычисления двумя способами.
Способ №1
Представим площадь искомой фигуры как сумму площадей отдельных фигур.
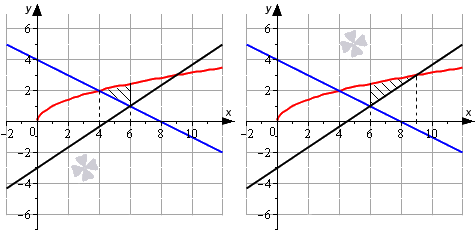
Тогда площадь фигуры равна:
Способ №2
Площадь исходной фигуры можно представить как сумму двух других фигур.
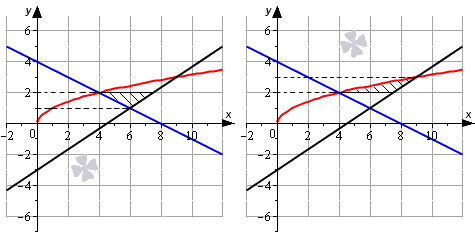
Тогда решим уравнение линии относительно , а только после этого применим формулу вычисления площади фигуры.
Таким образом, площадь равна:
Как видите, значения совпадают.
Ответ:
Итоги
Для нахождения площади фигуры, которая ограничена заданными линиями нам необходимо построить линии на плоскости, найти точки их пересечения, применить формулу для нахождения площади. В данном разделе мы рассмотрели наиболее часто встречающиеся варианты задач.
Навигация по статьям
