
Статью подготовили специалисты образовательного сервиса Zaochnik.
Вычитание натуральных чисел столбиком: примеры, решения
Содержание:
Существует удобный метод нахождения разности двух натуральных чисел – вычитание в столбик, или вычитание столбиком. Этот способ берет свое название от метода записи уменьшаемого и разности друг под другом. Так можно провести и основные, и промежуточные вычисления в соответствии с нужными разрядами чисел.
Этим методом удобно пользоваться, поскольку это очень просто, быстро и наглядно. Все сложные на первый взгляд подсчеты можно свести к сложению и вычитанию простых чисел.
Ниже мы рассмотрим, как именно пользоваться этим методом. Наши рассуждения будут подкреплены примерами для большей наглядности.
Что нужно повторить перед изучением вычитания столбиком?
Метод основан на некоторых простых действиях, которые мы уже разбирали ранее. Необходимо повторить, как правильно вычитать с помощью таблицы сложения. Также желательно знать основное свойство вычитания равных натуральных чисел (в буквенном виде оно записывается как ). Нам понадобятся следующие из него равенства и , где – любое произвольно взятое натуральное число (если требуется, посмотрите основные свойства нахождения разности целых чисел).
Кроме того, важно знать, как определять разряд натуральных чисел.
Разбор метода вычитания столбиком
Главное на первом этапе – правильно записать исходные данные. Для начала записываем первое число, из которого будем вычитать. Под ним располагаем вычитаемое. Цифры должны быть расположены строго одна под другой с учетом разряда: десятки под десятками, сотни под сотнями, единицы под единицами. Запись читается справа налево. Далее ставим минус с левой стороны от столбика и подводим черту под обоими числами. Под ней будет записываться конечный результат.
Покажем на примере, какая запись подсчета является правильной:
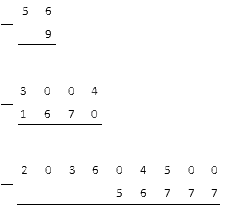
С помощью первой мы можем найти, сколько будет , с помощью второй – , третьей – .
Как видно, с помощью этого метода можно производить вычисления разной сложности.
Далее рассмотрим сам процесс нахождения разности. Для этого выполняем поочередное вычитание значений разрядов: сначала вычитаем единицы из единиц, потом десятки из десятков, потом сотни из сотен и т.д. Значения записываем под чертой, отделяющей исходные данные от результата. В итоге у нас должно получиться число, которое и будет верным ответом задачи, т.е. разностью исходных чисел.
Как именно выполняются подсчеты, можно увидеть на этой схеме:
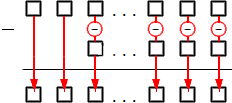
С общей картиной записи и подсчета мы разобрались. Однако в методе есть и некоторые моменты, нуждающиеся в уточнении. Для этого мы приведем конкретные примеры и поясним их. Начнем с простейших задач и будем постепенно наращивать сложность, пока наконец не разберем все нюансы.
Советуем внимательно прочитать все примеры, потому что каждый из них иллюстрирует отдельные непонятные моменты. Если вы дойдете до конца и запомните все объяснения, то подсчет разности натуральных чисел в дальнейшем не будет вызывать у вас ни малейших затруднений.
Условие: найдем разность с помощью вычитания столбиком.
Решение:
Запишем эти числа одно под другим, правильно расположив разряды друг под другом, и подчеркнем их:
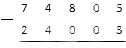
Вычитание начинается справа налево, то есть с единиц. Считаем: (если нужно, повторите таблицы сложения натуральных чисел). Итог запишем под чертой там, где указаны единицы:
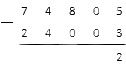
Вычитаем десятки. Оба значения в нашем столбике нулевые, а вычитание нуля из нуля всегда дает нуль (как вы помните, мы упоминали, что нам в дальнейшем потребуется это свойство вычитания). Результат записываем в нужное место:
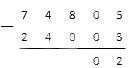
Далее считаем значения разности сотен: : . Вписываем итог следующим числом в наш будущий результат:
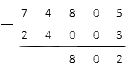
Следующий шаг – нахождение значения разности тысяч: . Получившийся нуль записываем на положенное ему место и получаем в итоге:
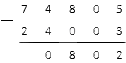
Нам остается подсчитать только разность между цифрами, означающими десятки тысяч. Пишем последнюю цифру под чертой и смотрим, что у нас вышло:
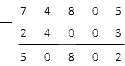
У нас получилось , которое и будет верным ответом для указанного выше примера. На этом вычисления завершены.
Ответ: .
Возьмем другой пример:
Условие: подсчитаем, сколько будет с помощью метода нахождения разности столбиком.
Решение:
Шаги, которые нам нужно сделать, мы уже приводили выше. Выполняем их последовательно для новых чисел и получаем в итоге:
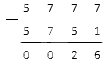
В начале результата стоит два нуля. Т.к. они стоят первыми, то можно смело их отбросить и получить в ответе . Это число и будет правильным ответом нашего примера.
Ответ: .
Если посмотреть на условия двух примеров, приведенных выше, легко заметить, что до сих пор мы брали только числа, равные по количеству знаков. Но метод столбика можно использовать и тогда, когда уменьшаемое включает в себя больше знаков, чем вычитаемое.
Условие: найдем разность число .
Решение
Запишем числа друг под другом, соблюдая нужную соотнесенность разрядов. Это будет выглядеть так:

Теперь поочередно вычисляем значения:
– единиц: ;
– десятков: ;
– сотен: ;
– тысяч: .
Запишем, что у нас получилось:
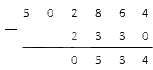
Вычитаемое имеет значения в месте десятков и сотен тысяч, а вот уменьшаемое нет. Что же делать? Вспомним, что пустота в математических примерах равнозначна нулю. Значит, нам нужно вычесть нули из исходных значений. Вычитание нуля из натурального числа всегда дает нуль, следовательно, все, что нам остается, – это переписать исходные значения разрядов в область ответа:
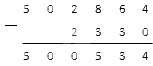
Наши подсчеты завершены. Мы получили итог: .
Ответ: .
В наших примерах значения разрядов вычитаемого всегда оказывались меньше, чем значения уменьшаемого, поэтому никаких трудностей при подсчете это не вызывало. Что делать, если из значения верхней строки нельзя вычесть значение нижней, не уйдя при этом в минус? Тогда нам нужно "взять взаймы" значения более старших разрядов. Возьмем конкретный пример.
Условие: найдите разность .
Пишем уже привычный нам столбик и делаем первый шаг вычислений: . Получаем:
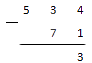
Далее нам надо перейти к подсчету десятков. Для этого нам надо из вычесть . Это действие с натуральными числами выполнить нельзя, ведь оно имеет смысл только при таком уменьшаемом, которое больше вычитаемого. Поэтому в данном примере нам нужно "занять" единицу из старшего разряда и тем самым "разменять" его. То есть мы как бы меняем на десяток и берем одну из них. Чтобы не забыть об этом, отметим нужный разряд точкой, а в десятках запишем другим цветом. У нас получилась запись следующего вида:
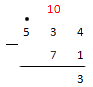
Далее нам надо добавить полученные десяток к трем, что у нас уже есть: , а потом уже из вычитаем :
.
Получившийся результат пишем на нужном месте под чертой:
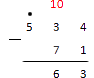
Нам осталось закончить подсчет, вычислив сотни. У нас стоит точка над числом : это значит, что мы отсюда брали десяток для предыдущего разряда. Тогда . От четверки же ничего отнимать не нужно, поскольку вычитаемое в разряде сотен значений не имеет. Записываем на место и получаем ответ:
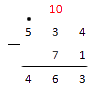
Ответ: .
Зачастую выполнять действие "размена" в рамках одного примера приходится несколько раз. Разберем такую задачу.
Условие: сколько будет ?
Решение
В первом же этапе подсчета надо вычесть двойку из семерки, так что сразу "занимаем" десятку для размена на единиц. Отмечаем это действие точкой и считаем . Вот как выглядит наша запись с отметками:
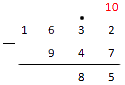
Далее нам надо подсчитать десятки. Указанная точка означает, что для вычислений мы берем в этом разряде число на единицу меньше: . Из двойки нам придется вычитать четверку, так что "размениваем" сотни. У нас получается .
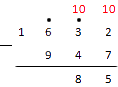
Движемся дальше к подсчету сотен. Из шестерки мы уже занимали единицу, так что . Из пятерки вычитаем девятку, для чего берем имеющуюся у нас тысячу и "размениваем" ее на сотен. Таким образом, . Теперь наша запись с примечаниями выглядит так:
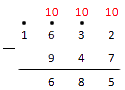
Нам осталось сделать подсчеты в тысячном разряде. Одну единицу отсюда мы уже занимали, так что . Пишем результат под итоговую черту и смотрим, что получилось:
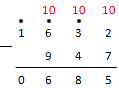
На этом вычисления закончены. Нуль в начале можно отбросить. Значит, .
Ответ: .
Возьмем еще более сложный пример.
Условие: вычтите из .
Решение
В первом шаге, как и ранее, нам приходится вычитать двойку из семерки. Идем в десятки за "разменом". Но у нас их нет, как нет и сотен: на месте этих разрядов у уменьшаемого стоят нули. Поэтому идем сразу в тысячу. Это сотен, так что:
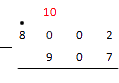
После этого одну сотню представляем в виде десяток:
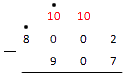
Финальное действие в "размене" – один десяток на единиц. Получим:
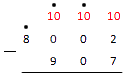
Только на этом этапе мы сможем наконец подсчитать сумму и вычесть из нее число . В итоге у нас будет 5. Поместим результат на нужное место:
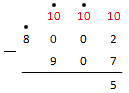
Теперь движемся к другим разрядам, отмеченным точками. Видим над десятками точку – считаем: . Прибавляем к нему значение разряда десятков уменьшаемого . Из результата надо вычесть значения разряда десятков вычитаемого . У нас вышло:
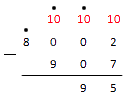
Далее над сотнями также видим точку. Считаем: . Прибавляем сотни числа и от результата отнимаем сотни . Получаем: . Теперь наша запись выглядит так:
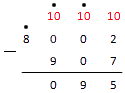
У нас остался последний шаг. Мы видим оставшееся число восемь с точкой, означающей, что ее надо уменьшить на единицу. Считаем число :
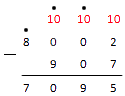
Ответ: .
Это были все сложные моменты, которые мы хотели пояснить. Они пригодятся для быстрых вычислений на практике. Завершим статью еще одним примером, но без комментариев:
Вычислите: .
Решение
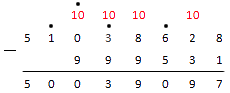
Ответ:
Навигация по статьям
