Умножение натуральных чисел: свойства, примеры

Содержание:

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Для операции умножения натуральных чисел $(ℕ)$ характерен ряд результатов, которые справедливы для любых умножаемых натуральных чисел. Эти результаты называются свойствами. В данной статье мы сформулируем свойства умножения натуральных чисел, приведем их буквенные определения и примеры.

Переместительное свойство умножения натуральных чисел

Переместительное свойство часто называют также переместительным законом умножения. По аналогии с переместительным свойством для сложения чисел, оно формулируется так:

Переместительный закон умножения

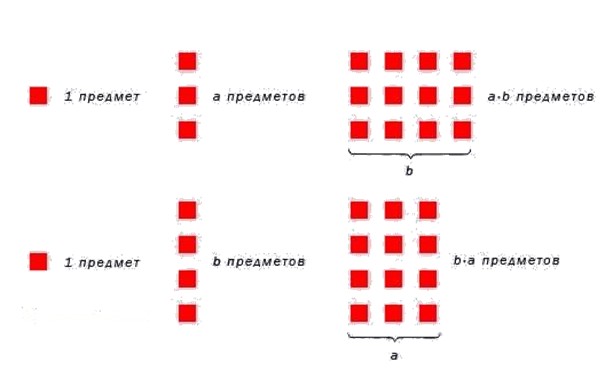
От перемены мест множителей произведение не меняется.

В буквенном виде переместительное свойство записывается так: $a \cdot b = b \cdot a$

$a$ и $b$ - любые натуральные числа.

Возьмем любые два натурльных числа и наглядно покажем, что данное свойство справедливо. Вычислим произведение $2 \cdot 6$ . По определению произведения, нужно число $2$ повторить $6$ раз. Получаем: $2 \cdot 6 = 2 + 2 + 2 + 2 + 2 + 2 = 12$ . Теперь поменяем множители местами. $6 \cdot 2 = 6 + 6 = 12$ . Очевидно, переместительный закон выполняется.

На рисунке ниже проиллюститруем переместительное свойство умножения натуральных чисел.

Переместительное свойство умножения натуральных чисел

Сочетательное свойство умножения натуральных чисел

Второе название для сочетательного свойства умножения - ассоциативный закон, или ассоциативное свойство. Вот его формулировка.

Сочетательный закон умножения

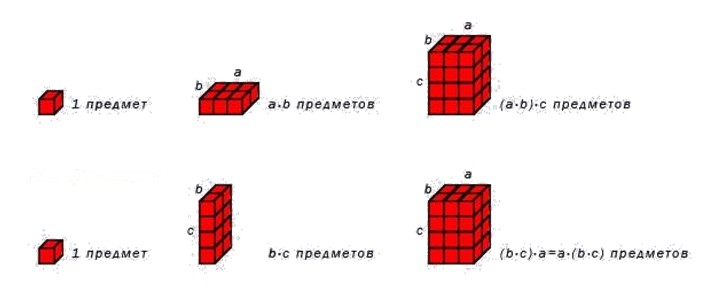
Умножение числа $a$ на произведение чисел $b$ и $c$ равносильно умножению произведения чисел $a$ и $b$ на число $c$ .

Приведем формулировку в буквенном виде:

$a \cdot (b \cdot c) = (a \cdot b) \cdot c$

$a, b, c$ - любые натуральные числа. Сочетательный закон работает для трех и более натуральных чисел.

Для наглядности приведем пример. Сначала вычислим значение $4 \cdot (3 \cdot 2)$ .

$4 \cdot (3 \cdot 2) = 4 \cdot 6 = 4 + 4 + 4 + 4 + 4 + 4 = 24$

Теперь переставим скобки и вычислим значение $(4 \cdot 3) \cdot 2$ .

$(4 \cdot 3) \cdot 2 = 12 \cdot 2 = 12 + 12 = 24$

$4 \cdot (3 \cdot 2) = (4 \cdot 3) \cdot 2$

Как видим, теория совпадает с практикой, и свойство справедливо.

Сочетательное свойство умножения также можно проиллюстрировать с помощью рисунка.

Сочетательное свойство умножения натуральных чисел

Распределительное свойство относительно умножения

Без распределительного свойста не обойтись, когда в математическом выражении одновременно присутствуют операции умножения и сложения. Это свойство определяет связь между умножением и сложением натуральных чисел.

Распределительное свойство умножения относительно сложения

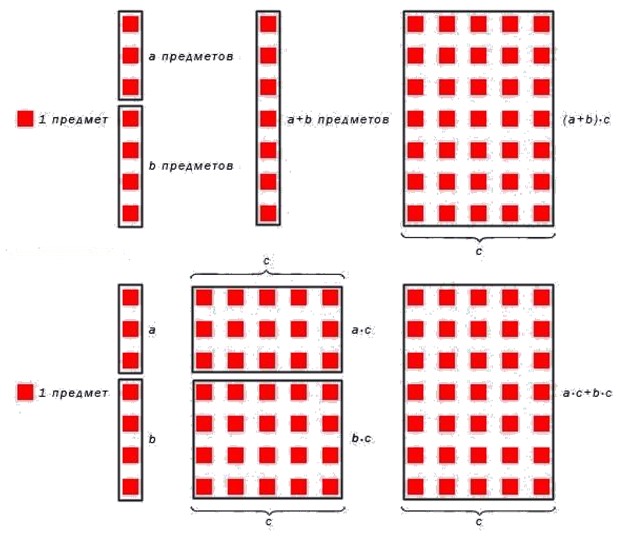
Умножения суммы чисел $b$ и $c$ на число $a$ равносильно сумме произведений чисел $a$ и $b$ и $a$ и $c$ .

Запишем в форме буквенного выражения:

$a \cdot (b + c) = a \cdot b + a \cdot c$

$a, b, c$ - любые натуральные числа.

Теперь на наглядном примере покажем, как работает это свойство. Вычислим значение выражения $4 \cdot (3 + 2)$ .

$4 \cdot (3 + 2) = 4 \cdot 3 + 4 \cdot 2 = 12 + 8 = 20$

С другой стороны $4 \cdot (3 + 2) = 4 \cdot 5 = 20$ . Справедливость распределительного свойства умножения относительно сложения показана наглядно.

Для лучшего понимания приведем рисунок, иллюстрирующий суть умножения числа на сумму чисел.

Распределительное свойство относительно умножения

Распределительное свойство умножения относительно вычитания

Распределительное свойство умножения относительно вычитания формулируется аналогично данному свойству относительно сложения, следует лишь учитывать знак операции.

Распределительное свойство умножения относительно вычитания

Умножения разности чисел $b$ и $c$ на число $a$ равносильно разности произведений чисел $a$ и $b$ и $a$ и $c$ .

Запишем в форме буквенного выражения:

$a \cdot (b - c) = a \cdot b - a \cdot c$

$a, b, c$ - любые натуральные числа.

В предыдущем примере заменим "плюс" на "минус" и запишем:

$4 \cdot (3 - 2) = 4 \cdot 3 - 4 \cdot 2 = 12 - 8 = 4$

С другой стороны $4 \cdot (3 - 2) = 4 \cdot 1 = 4$ . Таким образом, справедливость свойства умножения натуральных чисел относительно вычитания показана наглядно.

Умножение единицы на натуральное число

Умножение единицы на любое натуральное число в результате дает данное число.

$1 \cdot a = a$

По определению операции умножения, произведение чисел $1$ и $a$ равно сумме, в котором слагаемое $1$ повторяется $a$ раз.

$1 \cdot a = \sum_{i = 1}^{a} 1$

Умножение натурального числа $a$ на единицу представляет собой сумму, состоящую из одого слагаемого $a$ . Таким образом, переместительное свойство умножения остается справедливым:

$1 \cdot a = a \cdot 1 = a$

Умножение нуля на натуральное число

Число $0$ не входит в множество натуральных чисел. Тем не менее, есть смысл рассмотреть свойство умножения нуля на натуральное число. Данное свойство часто используется при умножении натуральных чисел столбиком.

Умножение нуля на натуральное число

Произведение числа $0$ и любого натурального числа $a$ равно числу $0$ .

$0 \cdot a = 0$ .

По определению, произведение $0 \cdot a$ равно сумме, в которой слагаемое $0$ повторяется $a$ раз. По свойствам сложения, такая сумма равна нулю.

В результате умножения единицы на нуль получается нуль. Произведение нуля на сколь угодно большое натуральное число также дает в результате нуль.

Напимер: $0 \cdot 498 = 0; 0 \cdot 9638854785885 = 0$

Справедливо и обратное. Произведение числа на нуль также дает в результате нуль: $a \cdot 0 = 0$ .

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.