
Статью подготовили специалисты образовательного сервиса Zaochnik.
Общее представление о делении натуральных чисел с остатком
Содержание:
В данном материале мы разберем, как разделить одно натуральное число на другое с остатком. Для начала сформируем общее представление о таком действии, определимся с терминами и обозначениями, а потом посмотрим, какие задачи можно решить с его помощью. В последнем пункте попробуем объяснить, какие связи существуют между понятиями делимого, делителя, неполного частного и остатка от деления.
Общее представление о делении с остатком
Ранее мы указывали, что сам процесс деления сводится к разъединению одного множества на два или несколько. Чаще всего мы встречаемся с делением на равные части, то есть множества, получившиеся в результате, будут одинаковыми. Но так разделить возможно далеко не всегда. К примеру, конфет разделить поровну на троих детей не выйдет: у каждого будет по конфеты, а две останутся лишними. В данном случае мы имеем остаток , то есть остались две конфеты. Этот пример отображает основной смысл деления с остатком. Запишем определение:
Разделить с остатком – значит представить исходное множество в виде некоторого числа равных множеств и еще одного дополнительного, элементов которого недостаточно для создания требуемого множества.
В чем состоит смысл деления с остатком?
В случае натуральных чисел деление с остатком имеет следующий смысл. Мы уже знаем, что понятие натурального числа тесно связано с количеством чего-либо. Допустим, у нас есть некое число предметов (обозначим его ), а после его деления образуется остаток, условно . У нас остались числа и . Есть два основных подхода к их обозначению:
1) если –количество элементов в каждом равном множестве, полученном после деления, то – это количество множеств, которое у нас получилось.
2) если – это количество множеств, то – это число предметов в каждом из них.
Поясним нашу мысль на конкретных числах. Допустим, натуральное число было разделено на . В итоге мы имеем два числа – и . Мы можем рассмотреть эту ситуацию с двух сторон:
1) тринадцать предметов были сгруппированы по . У нас получилось группы, а в исходном множестве остался всего предмет;
2) тринадцать предметов разложили по группам. У нас получилось, что в каждой группе по предмета, а остаток равен .
Если натуральное число всегда можно разделить с остатком на любое натуральное , то можно выделить следующие ситуации:
1. A можно разделить на без остатка, то есть все предметы можно разделить на равные множества. При этом «лишних» у нас не останется, тогда будет равно . Получается, что деление без остатка – это частный случай деления с остатком.
2. A может быть меньше . Тогда ни одного требуемого множества мы из него составить не можем, и число будет равно нулю, а остаток равен (то есть числу предметов в исходном множестве).
3. A может делиться на с остатком. Тогдазначения и будут натуральными числами.
Подводим итог:
Результат деления натуральных чисел и с остатком – это два числа и , которые либо оба являются натуральными, либо одно из них равно нулю.
Основные понятия, используемые при делении с остатком
Здесь мы определимся с основными терминами, которые будем использовать, если речь идет о делении с остатком.
То натуральное число, которое делят на части, принято называть делимым, а то, на которое делят – делителем. Получившиеся в результате два числа мы называем соответственно остатком и неполным частным. К примеру, если мы разделим на , то в итоге неполным частным будет , и остатком тоже .
Знак деления, используемый при решении примеров с остатком, аналогичен тому же знаку «разделить» (две точки, расположенные вертикально), что и при делении нацело. В некоторых источниках можно встретить обозначение «», смысл которого тот же самый. Так, числовое выражение означает деление одного натурального числа на другое с остатком.
Обозначим неполное частное буквой , остаток – , исходное число – , а делитель – . Тогда суть процесса деления в буквенном виде мы можем выразить как (ост. ).
Также можно записать это в виде схемы: делимое: делитель неполное частное (ост. остаток).
Из самого понятия о делении с остатком следует, что в любом случае остаток будет меньше делителя. Если бы он был равен ему или был нулевым, то это уже было бы деление нацело, поскольку у нас в итоге вышло бы несколько равных множеств.
Задачи, в которых используется деление с остатком
В результате процесса деления, описываемого в этой статье, всегда получаются два числа, одно из которых является остатком, а другое – неполным частным. Поэтому оно будет полезно для решения двух разных типов задач:
1. Нахождение количества необходимых равных множеств, которые можно составить из заданного количества предметов, или же количества предметов в равных множествах, полученных в результате деления.
Например:
У нас есть шаров, которыми мы будем наряжать елки. Если на каждую елку нужно шаров, сколько всего елок можно нарядить? Результат мы получим после деления с остатком.
Другой пример:
У нас есть книги, которые нужно упаковать в ящиков. Число книг, которое мы будем класть в каждую коробку, можно определить в результате деления на .
Вычислять мы можем не только количество предметов, но и изменения величин (массы, времени, длины и др.)
Например, на заводе произведено л молока. Его нужно разлить в бутылки по л. Мы можем вычислить неполное частное и понять, сколько бутылок будет в итоге. Или же если на производство какого-то изделия тратится часа, то мы можем найти, сколько можно их выпустить за один восьмичасовой рабочий день.
2. Задачи второго типа направлены на вычисление количества предметов в исходном множестве, которые остались после деления. Это могут быть не только предметы, но и величины.
Например:
У нас есть конфет, которые раскладываются по коробкам. Мы знаем число этих коробок – оно равно . Деление на подскажет нам, сколько конфет остались неупакованными.
Чтобы изготовить бетонную плиту, надо израсходовать кг цемента. Если мы закупили кг, на сколько плит нам хватит? Результат мы вычислим в результате деления с остатком.
Основные связи между понятиями делимого, делителя, неполного частного и остатка от деления
Для установления этих связей сразу разберем конкретный пример.
У нас есть некоторое множество предметов, обозначим его буквой . Распределим его по кучкам, количество которых равно . Всего в каждой кучке у нас будет c предметов. Остаток обозначим . В буквенном виде это выражение можно записать как (ост. ). Теперь проанализируем связи, которые есть в этом равенстве.
Если у нас есть значения делителя, неполного частного и остатка, мы можем найти делимое. Если мы объединим все имеющиеся кучки и добавим к ним остаток, то получим множество из исходного количества предметов.
Учитывая смысл умножения и сложения натуральных чисел, мы можем записать это в виде равенства . А наличие у умножения и сложения переместительных свойств позволяет нам переформулировать его как . Получается следующее правило:
Чтобы найти делимое, нужно сложить остаток с произведением делителя на неполное частное.
Верное равенство, полученное в итоге, будет полезно для решения задач с неизвестным делимым, то есть таких, где нужно найти исходное число предметов. Приведем пример:
Вычислите делимое, если неполное частное равно одиннадцати, остаток двум, а делитель семи.
Решение
Имеем , и . Это все данные, которые нам нужны для вычислений. Подставим нужные значения: . Следуя правильному порядку выполнения математических действий, получим в итоге (если нужно, повторите основы умножения и сложения натуральных чисел).
Ответ: делимое будет равно .
Если нужно проверить верность результата действия деления с остатком, то для этого мы также проверяем справедливость равенства .
Если нам известны значения делимого, делителя и неполного частного, то мы можем найти остаток.
Вспомним, что остаток от деления, который мы выше договорились обозначить буквой , представляет собой число элементов, оставшееся в исходном множестве после его разделения на равные части. Значит, . Записать это равенство мы можем благодаря свойствам умножения и вычитания натуральных чисел. Сформулируем определение:
Чтобы найти остаток от деления одного натурального числа на другое, нужно вычесть из делимого произведение делителя на неполное частное.
У нас получилось буквенное выражение , которое будет нам полезно при нахождении остатка от деления. Разберем такую задачу.
Мы разделили на и получили неполное частное . Вычислите остаток от деления.
Решение
Имеем , , . Если мы подставим в выражение исходные значения, то сможем подсчитать остаток: . Поскольку , то .
Ответ: остаток от деления равен .
Мы также можем найти неполное частное, если знаем значение делимого, делителя и остатка. Исключим из исходного множества те элементы, которые образуют остаток. Благодаря свойствам вычитания натуральных чисел количество элементов в множестве мы теперь можем записать как . После этого уже можно произвести деление без остатка, в результате которого получится множеств по c элементов в каждом. Мы получили равенство . Его также можно записать в виде .
Если нужно найти неполное частное, нужно из делимого вычесть остаток и результат разделить на делитель.
Мы разделили на и получили остаток . Вычислите неполное частное.
Решение
Отнимем остаток от делимого и результат разделим на делитель. Считаем: (для подсчета мы использовали метод подбора частного).
Ответ: неполное частное равно .
Осталось разобрать последний случай: как быть, если нужно найти делитель при известных значениях делимого, остатка и неполного частного? Начнем опять же с исключения остатка из делимого, то есть запишем . Вспомнив смысл деления одного натурального числа на другое, запишем следующее равенство: . Также будет верно . Сформулируем правило:
Найти делитель можно, если вычесть из делимого остаток и получившуюся разность разделить на неполное частное.
Возьмем пример решения такой задачи.
Было выполнено деление на некоторое число с остатком , неполное частное при этом составило . Найдите значение делителя.
Решение
Вычтем остаток из делимого и получим . Результат нужно разделить на известное нам неполное частное . В итоге получится нужное нам значение делителя. Вычислим столбиком:
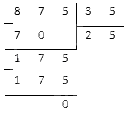
Ответ: делитель равен .
Навигация по статьям
