
Статью подготовили специалисты образовательного сервиса Zaochnik.
Деление отрицательных чисел: правило и примеры
Содержание:
В данной статье дадим определение деления отрицательного числа на отрицательное, сформулируем и обоснуем правило, приведем примеры деления отрицательных чисел и разберем ход их решения.
Деление отрицательных чисел. Правило
Напомним, в чем суть операции деления. Данное действие представляет собой нахождение неизвестного множителя по известному произведению и известному другому множителю. Число называется частным от деления чисел и , если верно произведение . При этом, .
Частное ои деления одного отрицательного числа на другое отрицательное число равно частному от деления модулей этих чисел.
Пусть и - отрицательные числа. Тогда
.
Данное правило сводит деление двух отрицательных чисел к делению положительных чисел. Оно справедливо не только для целых чисел, но также для рациональных и действительных чисел. Результат деления отрицательного числа на отрицательное есть всегда положительное число.
Приведем еще одну формулировку данного правила, подходящую для рациональных и действительных чисел. Она дается с помощью взаимно-обратных чисел и гласит: для деления отрицательного числа на число undefined умножить на число , обратное числу .
.
Это же правило, сводящее деление к умножению, можно применять также и для деления чисел с разными знаками.
Равенство a ÷ b = a · b - 1 можно доказать, используя свойство умножения действительных чисел и определение взаимно обратных чисел. Запишем равенства:
.
В силу определения операции деления, данное равенство доказывает, что есть частное от деления числа на число b.
Перейдем к рассмотрению примеров.
Деление отрицательных чисел. Примеры
Начнем с простых случаяв, переходя к более сложным.
Разделим на .
Модули делителя и делимого соответственно равны и . Запишем:
.
Разделим на .
Аналогично, записываем по правилу:
.
Такой же результат получится, если использовать вторую формурировку правила с обратным числом.
.
Деля дробные рациональные числа удобнее всего представлять их в виде обыкновенных дробей. Однако, можно делить и конечные десятичные дроби.
Разделим на .
Сначала записываем модули этих чисел: и .
Теперь можно выбрать один из двух способов:
- Разделить десятичные дроби столбиком.
- Перейти к обыкновенным дробям и выполнить деление.
Разберем оба способа.
1. Выполняя деление десятичных дробей столбиком, перенесем запятую на две цифры вправо.
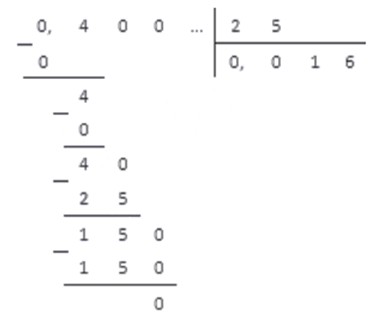
Ответ:
2. Теперь приведем решение с переводом десятичных дробей в обыкновенные.
Полученные результаты совпадают.
В заключение отметим, что если делимое и делитель являются иррациональными числами и задаются в виже корней, степеней, логарифмов и т.д., результат деления записывается в виде числового выражения, приблизительное значение которого вычисляется в случае необходимости.
Вычислим частное от деления чисел и .
=.
Навигация по статьям
