
Статью подготовили специалисты образовательного сервиса Zaochnik.
Деление десятичных дробей: правила, примеры, решения
Содержание:
В этой статье мы разберем такое важное действие с десятичными дробями, как деление. Сначала сформулируем общие принципы, затем разберем, как правильно выполнять деление десятичных дробей столбиком как на другие дроби, так и на натуральные числа. Далее мы разберем деление обыкновенных дробей на десятичные и наоборот, а в конце посмотрим, как правильно выполнять деление дробей, заканчивающихся на и др.
Здесь мы возьмем только случаи с положительными дробями. Если же перед дробью стоит минус, то для действия с ней нужно изучить материал о делении рациональных и действительных чисел.
Основы деления десятичных дробей
Все десятичные дроби, как конечные, так и периодические, представляют из себя всего лишь особую форму записи обыкновенных дробей. Следовательно, на них распространяются те же принципы, что и на соответствующие им обыкновенные дроби. Таким образом, весь процесс деления десятичных дробей мы сводим к замене их на обыкновенные с последующим вычислением уже известными нам способами. Возьмем конкретный пример.
Разделите на .
Решение
Запишем десятичные дроби в виде обыкновенных. У нас получится:
.
Таким образом, нам надо разделить на . Считаем:
Из получившейся в итоге неправильной дроби можно выделить целую часть и получить смешанное число , а можно представить ее в виде десятичной дроби, чтобы она соответствовала исходным цифрам: . О том, как это сделать, мы уже писали ранее.
Ответ: .
Посчитайте, сколько будет .
Решение
Для начала нам нужно перевести периодическую десятичную дробь в обыкновенную.
После этого конечную десятичную дробь также переведем в другой вид: . Теперь у нас есть два числа, с которыми нам будет легко провести необходимые вычисления:
У нас получился результат, который мы также можем перевести в десятичный вид. Для этого разделим числитель на знаменатель, используя метод столбика:
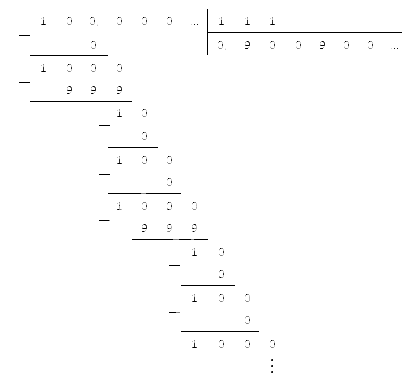
Ответ: .
Если же в примере на деление нам встретились непериодические десятичные дроби, то мы будем действовать немного иначе. Мы не можем их привести к привычным обыкновенным дробям, поэтому при делении приходится предварительно округлять их до определенного разряда. Это действие должно быть выполнено как с делимым, так и с делителем: имеющуюся конечную или периодическую дробь в интересах точности мы тоже будем округлять.
Найдите, сколько будет .
Решение
Первым делом мы округляем обе дроби до сотых. Так мы переходим от бесконечных непериодических дробей к конечным десятичным:
Можем продолжить подсчеты и получить примерный результат: .
Точность результата будет зависеть от степени округления.
Ответ: .
Как разделить натуральное число на десятичную дробь и наоборот
Подход к делению в этом случае практически аналогичен: конечные и периодические дроби заменяем обыкновенными, а бесконечные непериодические округляем. Возьмем для начала пример деления с натуральным числом и десятичной дробью.
Разделите на .
Решение
Приведем к виду обыкновенной дроби: . Далее нам надо просто разделить ее на натуральное число. Делать это мы уже умеем:
Если перевести результат в десятичную запись, то мы получим .
Ответ: .
Как разделить десятичную дробь на натуральное число столбиком
Метод деления столбиком хорош не только для натуральных чисел. По аналогии мы можем использовать его и для дробей. Ниже мы укажем последовательность действий, которую нужно для этого осуществить.
Для деления столбиком десятичных дробей на натуральные числа необходимо:
1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
2. Разделить столбиком десятичную дробь на натуральное число, используя алгоритм. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.
Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться, то ответом будет периодическая дробь.
Возьмем для примера несколько задач и попробуем выполнить эти шаги уже с конкретными числами.
Вычислите, сколько будет .
Решение
Используем метод столбика. Для этого допишем к дроби два нуля и получим десятичную дробь , которая будет равна исходной. Теперь пишем столбик для деления на :

Полученное число и будет нужным нам результатом деления целой части. Ставим запятую, отделяя ее, и продолжаем:
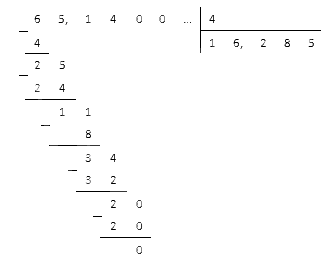
Мы добрались до нулевого остатка, следовательно, процесс деления завершен.
Ответ: .
Разделите на .
Решение
Делим сначала дробную часть и получаем:
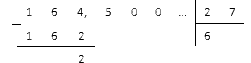
Отделяем полученную цифру запятой и продолжаем делить:

Мы видим, что остатки стали периодически повторяться, и в частном стали чередоваться цифры девять, два и пять. На этом мы остановимся и запишем ответ в виде периодической дроби .
Ответ: .
Как разделить столбиком одну десятичную дробь на другую
Такое деление можно свести к уже описанному выше процессу нахождения частного десятичной дроби и натурального числа. Для этого нам потребуется умножить делимое и делитель на и др. так, чтобы делитель превратился в натуральное число. Дальше выполняем описанную выше последовательность действий. Такой подход возможен благодаря свойствам деления и умножения. В буквенном виде мы записывали их так:
и так далее.
Сформулируем правило:
Для деления одной конечной десятичной дроби на другую необходимо:
1. Перенести запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, допишем в него нули с правой стороны.
2. После этого делим дробь столбиком на получившееся натуральное число.
Разберем конкретную задачу.
Разделите на .
Решение: Чтобы делитель стал натуральным числом, нам надо перенести запятую на один знак вправо. Так мы перешли к делению десятичной дроби на . Запишем полученные числа столбиком и вычислим
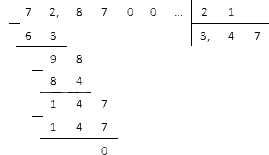
Ответ:
Вычислите .
Решение
Нам придется переносить запятую на три знака. В делителе для этого не хватит цифр, значит, нужно воспользоваться дополнительными нулями. Считаем, что получится в итоге:
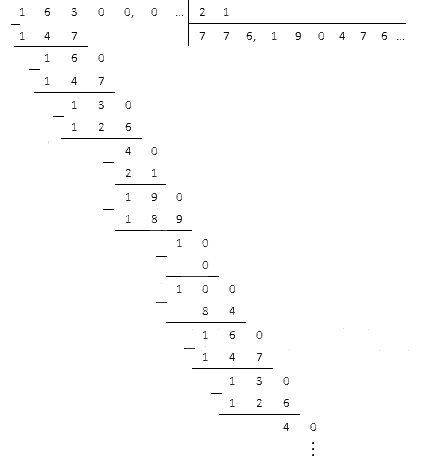
Видим периодическое повторение остатков . В частном повторяются и . Тогда наш результат является периодической десятичной дробью .
Ответ:
Описанный нами метод позволяет делать и наоборот, то есть делить натуральное число на конечную десятичную дробь. Посмотрим, как это делается.
Подсчитайте, сколько будет .
Решение
Очевидно, что нам придется перенести запятую вправо на один знак. После этого мы можем приступить к делению на . Запишем данные столбиком и вычислим результат:
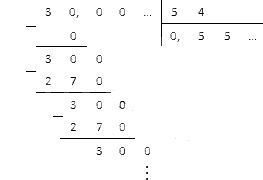
Повторение остатка дает нам в итоге число , которое является периодической десятичной дробью.
Ответ: .
Как разделить десятичные дроби на 1000, 100, 10 и др.
Согласно уже изученным правилам деления обыкновенных дробей, деление дроби на десятки, сотни, тысячи аналогично ее умножению на и др. Получается, чтобы выполнить деление, в данном случае достаточно просто перенести запятую на нужное количество цифр. Если значений в числе не хватит для переноса, нужно дописать нужное количество нулей.
Так, , а.
В случае с бесконечными десятичными дробями мы поступаем таким же образом.
Например, и
Как разделить десятичные дроби на 0,001, 0,01, 0,1 и др.
Воспользовавшись тем же правилом, мы можем так же разделить дроби на указанные значения. Это действие будет аналогично умножению на соответственно. Для этого мы переносим запятую на одну, две или три цифры в зависимости от условий задачи и дописываем нули, если цифр в числе окажется недостаточно.
К примеру, и .
Это правило действует и в случае с бесконечными десятичными дробями. Советуем только быть внимательными с периодом дроби, которая получается в ответе.
Так, , поскольку после того, как мы перенесли запятую в записи десятичной дроби на два знака вправо, у нас получилось
Если же у нас в примере непериодические дроби, то все обстоит проще:
Как разделить смешанное число или обыкновенную дробь на десятичную и наоборот
Это действие мы также сводим к операциям с обыкновенными дробями. Для этого надо заменить десятичные числа соответствующими обыкновенными дробями, а смешанное число записать в виде неправильной дроби.
Если мы делим непериодическую дробь на обыкновенную либо на смешанное число, нужно поступить наоборот, заменив обыкновенную дробь или смешанное число соответствующей им десятичной дробью.
Навигация по статьям
